paths on a graph
- Auteur:
- chris cambré
- Onderwerp:
- Grafiek
Try to make a 'walk' passing just once in any of the four points.
Can you create walks that look totally different? Experiment in following applet.
Click on the Pen Tool and draw your walk.
path
A path is a sequence of points connected by a sequence of lines.
(For further information see graph theory or Eulerian path )
There are open and closed paths:
Open path
Een open path starts and ends in two different points:
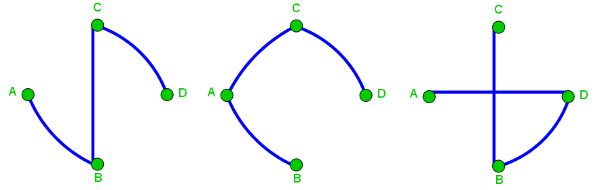
closed path
A closed path starts and ends in the same point. You can start in any point on the graph.
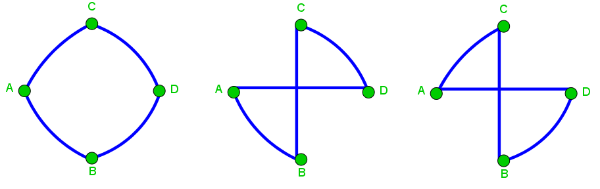
degree of a point
The degree of a point on a graph is the number of lines that come together in this point. Whether an Euler path is possible or not, depends on these degrees.
An Euler path is only possible if zero or two points of the graph have an odd degree.
- If two points have an odd degree than the walk has to start on one of these odd points and end in the other. The result is an open path.
- If zero points have an odd degree, then the walk can start anywhere and ends in the starting point. The result is a closed path.
In next applet you can make or brake connections between points by clicking on them, with a maximum of two between any two points.
Eventually you can build new bridges or or close existing ones. Try to establish an Eulerpad with as less changes as possible.
Create a graph with an open or closed path and try you walk by chosing a starting point and then dragging the red point. Examin the conditions to have open and closed path.