Disequazioni di II grado
Una disequazione di II grado si presenta sotto la forma , con .
Analizziamo i due metodi di risoluzione delle disequazioni di II grado, quello algebrico e quello grafico.
Metodo algebrico
Anzitutto, verifichiamo che a sia maggiore di 0. Nel caso in cui non lo fosse, basta cambiare segno a tutti i coefficienti della disequazione, nonché il suo verso. A questo punto, si risolve l'equazione associata:
che, come sappiamo, a seconda del valore di , può avere un numero di soluzioni compreso tra 0 e 2.
Le soluzioni della disequazione sono date dalla seguente tabella:
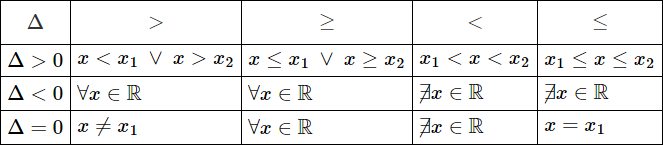

Quali sono le soluzioni della disequazione ?
Metodo grafico
Nel piano cartesiano un'equazione di secondo grado è rappresentata da una parabola e le sue soluzioni non sono altro che le intersezioni della parabola con l'asse delle ascisse. Dunque, studiando il grafico di una parabola, possiamo risolvere la disequazione di secondo grado ad essa associata senza effettuare calcoli algebrici.
Muovi i cursori di a, b e c e verifica cosa accade
Osservando la parabola originale della precedente sezione, determina le soluzioni della disequazione senza effettuare calcoli algebrici
Approfondimento
Osserviamo che il segno del coefficiente del termine di grado più alto, ossia a, determina il verso della concavità della parabola, che è rivolta verso l'alto se a>0, altrimenti è rivolta verso il basso.
Prestiamo attenzione al fatto che dal punto di vista algebrico è del tutto equivalente risolvere una disequazione con a<0, oppure con a>0 cambiando tutti i segni e il verso.
Anche dal punto di vista grafico, le soluzioni delle due disequazioni sono equivalenti. Come sono le parabole che rappresentano le 2 disequazioni?