Verifiche formali di limiti e teoremi
Questo capitolo tratta il tema dei limiti da un punto di vista piuttosto avanzato. Fornisce infatti esempi svolti di verifiche formali di limiti, e mostra come attraverso questo procedimento sia possibile dimostrare proprietà generali dei limiti.
VERIFICA DI UN LIMITE IN CUI SI RICAVA UN'ESPRESSIONE PER
Consideriamo il seguente limite
Formuliamolo in termini logico algebrici: se vogliamo che il risultato si avvicini abbastanza a 3, basta che la sia abbastanza vicina a 8
La parte in rosso riguarda l'avvicinamento lungo le (i risultati), mentre le parti in blu riguarda quelle lungo le (i valori di input).
Partiamo dalla condizione rossa, ovvero il risultato che vogliamo ottenere
Dobbiamo arrivare a dire che questa condizione è equivalente a quella blu, quindi dobbiamo isolare la . Eleviamo tutto alla seconda per sbarazzarci della radice, non prima di aver verificato che:
- la radice esiste: OK! consideriamo vicine a 8, quindi è positivo
- i segni coerenti: OK! l'unica quantità che potrebbe essere negativa è , ma stiamo considerando piccoli, quindi ragionevolmente minori di 3
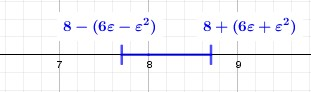
Se vogliamo trovare un raggio che garantisca di essere entro la zona blu in entrambe le direzioni, sarà sufficiente prendere il raggio minore dei due
In questo caso, per evidenti motivi, il raggio minore - e che quindi garantisce sufficiente vicinanza ad 8, è .
Abbiamo quindi verificato che se vogliamo che il risultato di disti da 3 meno di , questo è equivalente a dire che basta considerare che distino da 8 meno di .
VERIFICA DI UN LIMITE IN CUI NON SI RIESCE A DARE UN'ESPRESSIONE A
Consideriamo il seguente limite
Formuliamolo in termini logico algebrici: se vogliamo che il risultato si avvicini abbastanza a 12, basta che la sia abbastanza vicina a 3
La parte in rosso riguarda l'avvicinamento lungo le (i risultati), mentre le parti in blu riguarda quelle lungo le (i valori di input).
Partiamo dalla condizione rossa, ovvero il risultato che vogliamo ottenere
Si tratta di una catena di disequazioni di secondo grado, che vanno risolte con il metodo della parabola; ci conviene quindi spezzarle nel sistema equivalente
Abbiamo usato il colore blu per mettere in evidenza che vi è un termine in e tutto il resto è un termine noto, anche se "un po' strano" perché vi compare la ; nella seconda disequazione abbiamo raccolto un per mettere ancora più in evidenza questo termine.
Ognuna di queste disequazioni si risolve con il metodo della parabola. Partiamo della prima: si tratta di una parabola rivolta verso l'alto che tocca l'asse delle in
Essendo interessati alla parte in cui la parabola è negativa dobbiamo prendere i valori interni.
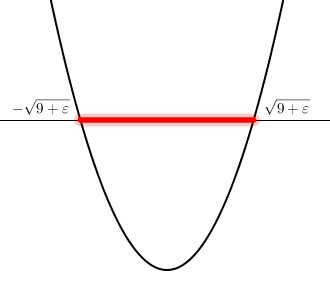
Svolgendo calcoli analoghi con la seconda disequazione troviamo una parabola ancora rivolta verso l'alto, che questa volta vale zero per
Questa volta però siamo interessati ai valori che rendono positiva la parabola, e quindi dobbiamo prendere quelli esterni. Mettendo a sistema i due risultati otteniamo
![Da notare che [math]\textcolor{blue}{\sqrt{9-\varepsilon}}[/math] viene PRIMA di [math]\textcolor{red}{\sqrt{9+\varepsilon}}[/math] perchè è un po' più piccolo. Per lo stesso motivo [math]\textcolor{blue}{-\sqrt{9-\varepsilon}}[/math] è meno negativo del corrispondente termine rosso e quindi è maggiore (ed è collocato alla sua destra).](https://www.geogebra.org/resource/ytdp7zvb/uTKLdlYNanWnujUH/material-ytdp7zvb.png)
Quindi affichè il risultato della funzione sia sufficientemente vicino a 12 la x deve essere in uno dei due intervalli verdi. Dato che ci interessa il caso in cui , concentriamoci sull'intervallo che presenta estremi positivi (le radici senza il meno):
In questo caso non è semplice esprimere questo intervallo l'insieme di valori che vanno da "3 meno un certo raggio " e "3 più lo stesso raggio - ricorda che la radice di una somma NON è la somma delle due radici, e cioè ad esempio .
Ci conviene quindi semplicemente verificare che questa scrittura equivale a dire che si trova in un certo intorno di , senza cercare di capire quale intorno. Questa operazione è più facile perché infatti è comunque appena più di , mentre è appena di meno (anche se non sappiamo quanto).
Un approccio alternativo è verificare che è sicuramente incluso tra questi due estremi, infatti se scriviamo
elevando al quadrato abbiamo
che, essendo positivo, è senz'altro vero. Quindi l'intervallo che contiene la contiene sicuramente anche il , e quindi è un intorno di .
Quindi abbiamo dimostrato che affermare che il risultato è in un intorno di 12 equivale a dire che è in un intorno di 3, e che quanto più vogliamo il risultato vicino a 12, quanto più vicino dovrà essere a 3. Il limite è quindi vero.
ATTENZIONE: abbiamo visto che la verifica ci ha rivelato che il risultato della funzione si avvicina a anche quando la si trova nell'altro intervallo verde, cioè
Puoi verificare, in modo del tutto analogo a quanto fatto sopra, che questo intervallo è un intorno di . Infatti la funzione tende a sia quando tende a che a . La corretta applicazione del concetto di limite ci ha quindi rivelato delle proprietà aggiuntive della funzione, oltre a quella che stavamo verificando.
TEOREMI SUI LIMITI
Utilizziamo ora la verifica formale dei limiti per dimostrare proprietà generali dei limiti, cioè non riferite ad una funzione particolare.
LIMITE DI UNA FUNZIONE MOLTIPLICATA PER UNA COSTANTE.
Consideriamo una funzione che si ottiene moltiplicando un'altra funzione per una costante , cioè . Vogliamo dimostrare che
Detto in altri termini, per calcolare il limite di basta moltiplicare per il limite di . In termini ancora più diretti, se una funzione è moltiplicata per una costante, si può portare fuori la costante fuori dal limite (sempre moltiplicandola).
Un esempio di applicazione di questo teorema ci permette di calcolare
Dimostrazione
Le nostre ipotesi sono che
riscriviamo esplicitamente la ipotesi 2 (usiamo i simboli e per sottolineare che si tratta dei raggi definiti per il limite della funzione :
Vogliamo dimostrare che queste due condizioni sono sufficienti a dimostrare che allora vale la tesi, cioè che ; utilizzando la ipotesi 1 possiamo riscriverla come
che scritta in forma esplicita (usiamo un'analoga notazione per indicare i raggi relativi ai limiti della funzione )diventa
Abbiamo chiarito tutti gli elementi del teorema, siamo pronti a costruirne la dimostrazione.
Partiamo dall'ipotesi 2: essa afferma che se prendiamo in un intorno di possiamo essere sicuri che
Dato che da qui vogliamo dimostrare che (TH1) è vera, per avvicinarci ad essa moltiplichiamo tutto per . Per il momento supponiamo che sia , così non dobbiamo invertire il verso delle disequazioni (puoi verificare che se prendiamo il caso in cui bisogna invertire il verso delle disequazioni, ma si giunge ad una conclusione identica).
Vediamo che se definiamo otteniamo esattamente
che è la tesi finale richiesta dalla (TH1). Quindi abbiamo visto che se consideriamo una appartenente ad un intorno di , il risultato di rientra in un intorno di .
In particolare per ottenere risultati che distino da meno di dobbiamo prendere lungo le un raggio pari a .
LIMITE DELLA SOMMA DI DUE FUNZIONI.
Consideriamo una funzione il cui risultato si ottiene sommando quello di due funzioni; ad esempio sia . Vogliamo dimostrare che il limite di quando coincide con la somma dei limiti di e .
Formuliamo subito il teorema nelle sue ipotesi e tesi.
Le nostre ipotesi sono che
mentre la tesi è
cioè, utilizzando l'ipotesi 1),
In termini espliciti, vogliamo quindi dimostrare che
Iniziamo la dimostrazione.
Riscriviamo le ipotesi 2 e 3 in modo esplicito, una sotto l'altra (usiamo due colori diversi per distinguerle meglio :
Da notare che partiamo dallo stesso (lo scegliamo noi) ma ogni funzione ad esso associa un diverso, dato che ogni funzione è fatta in modo diverso - puoi vederlo meglio nell'immagine qui sotto. In ogni caso se consideriamo entrambi i limiti saranno soddisfatti, quindi entrambe le catene di disequazioni finali saranno vere.
![Quando x tende a [math]x_0[/math], [math]f(x)[/math] tende a [math]L_f[/math] e [math]g(x)[/math] tende a [math]L_g[/math].[color=#00ff00]
Perché il risultato di [math]f[/math] cada nell'intervallo verde chiaro[/color], [color=#38761d][math]x[/math] deve essere nell'intervallo verde scuro di raggio [math]\delta_f[/math][/color].
[color=#ff7700]Perchè il risultato di [math]g[/math] cada nell'intervallo arancio[/color], [color=#38761d][math]x[/math] [/color][color=#ff0000]deve essere nell'intervallo rosso di raggio [math]\delta_g[/math][/color].
Se prendiamo [math]x[/math] nell'intervallo più piccolo dei due (che in questo esempio è quello rosso), entrambe le condizioni sono garantite.](https://www.geogebra.org/resource/rpsgs6kz/eu8hUzRgp5UfcIAI/material-rpsgs6kz.png)
Sommandole membro a membro otteniamo
Vediamo che definendo otteniamo
che non è altro che la tesi (TH2) che volevamo dimostrare.
Abbiamo quindi ottenuto che se vogliamo per la funzione somma un risultato vicino a meno di un certo è sufficiente considerare una distante al più un raggio .