Superficies (Colección)
 Caracola completa |  Caracola "abierta" |
 Toro completo |  Toro "abierto" |
- Superficie: objeto geométrico que posee dos dimensiones, es decir, cada uno de sus puntos espaciales de 3 coordenadas se puede definir usando sólo dos parámetros. Un poliedro es un sólido cuya superficie consta de caras planas. No incluiremos este tipo de superficies planas aquí (tampoco incluiremos el plano ni el círculo), pues ahora nos interesan las superficies con algún tipo de curvatura, ya sea local o global.
- Generatriz: también podemos definir una superficie como el lugar geométrico de las posiciones sucesivas de una línea que se mueve en el espacio siguiendo una ley determinada y continua. La línea anterior recibe el nombre de generatriz.
- Superficie cerrada: es la superficie exterior de un objeto con volumen. Divide el espacio en dos zonas, una acotada y otra no acotada. Ejemplos: esfera, toro, elipsoide, cualquier poliedro. (Esta definición sólo es válida en el espacio de tres dimensiones; para dimensiones mayores, se dice que una superficie es cerrada cuando no tiene "frontera", es decir, borde. Ejemplo: la botella de Klein.)
- Superficie abierta: la que no es cerrada. Ejemplos: cilindro, cono, hiperboloide.
- Sección plana: intersección de la superficie con un corte plano. Aquí llamaremos a estos cortes simplemente "secciones" (supondremos que los cortes son planos).
- Superficie cónica o cuádrica: corresponde a una ecuación de segundo grado en tres variables. Sus secciones son curvas cónicas (circunferencia, elipse, parábola o hipérbola). Pueden tener centro de simetría (esfera, cono, elipsoide, hiperboloide) o no tenerlo (cilindro, paraboloide elíptico, paraboloide hiperbólico).
- Superficie de revolución: aquella que se obtiene al hacer girar la generatriz alrededor de un eje. Ejemplos de revolución de rectas: cilindro, cono, hiperboloide. Ejemplos de revolución de curvas: esfera, catenoide, elipsoide, paraboloide, pseudoesfera, toro, sombrero de Sherlock.
- Superficie reglada: superficie que puede crearse a partir de una generatriz recta.
- Superficie reglada desarrollable: superficie en la que todos los puntos de una generatriz cualquiera poseen el mismo plano tangente (que contiene a esa generatriz). Ejemplos: cilindro, cono. Intuitivamente, superficie que se puede construir doblando papel sin arrugarlo; o, si se prefiere, extender en un plano realizando algunos cortes con tijeras.
- Superficie reglada alabeada: superficie reglada no desarrollable. Ejemplo: helicoide.
- Superficie doblemente reglada: superficie alabeada en la cual por cada uno de sus puntos pasan dos generatrices rectas (ejemplos: paraboloide hiperbólico, hiperboloide de una hoja).
|
| ||
|
|
| |
|
|
| |
|
|
|
|
|
| ||
|
|
| |
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
|
| ||
|
| ||
|
| ||
|
|
|
|
|
|
| |
|
| ||
|
|
| |
|
|
|
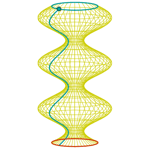 Aislante
Aislante
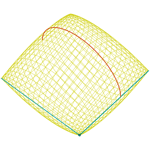 Almohada
Almohada
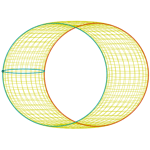 Bohemia
Bohemia
 Bola anidada
Bola anidada
 Bonete cruzado
Bonete cruzado
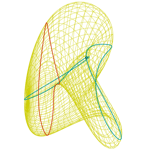 Boy
Boy
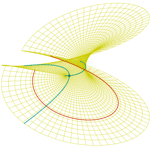 Catalan
Catalan
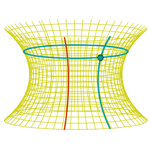 Catenoide
Catenoide
 Cilindro
Cilindro
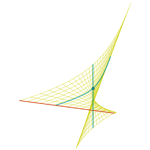 Cola de golondrina
Cola de golondrina
 Concha 1
Concha 1
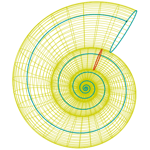 Concha 2
Concha 2
 Concha 3
Concha 3
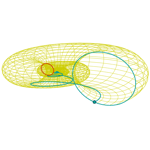 Concha 4
Concha 4
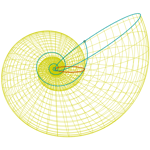 Concha 5
Concha 5
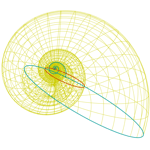 Concha 6
Concha 6
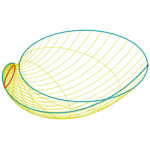 Concha 7
Concha 7
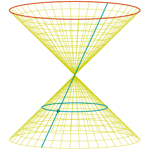 Cono
Cono
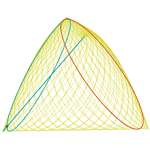
 Conoide recto
Conoide recto
 Cornucopia
Cornucopia
 Coseno
Coseno
 Cubo hiperbólico
Cubo hiperbólico
 Cuerno
Cuerno
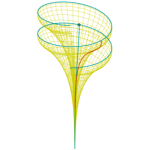 Dini
Dini
 Dupin
Dupin
 Elipsoide
Elipsoide
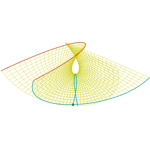 Enneper
Enneper
 Esfera
Esfera
 Esfera retorcida
Esfera retorcida
 Esfera de torsión
Esfera de torsión
 Esferas escaladas
Esferas escaladas
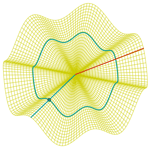 Flor
Flor
 Folium
Folium
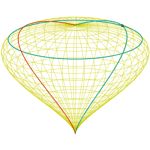 Gota
Gota
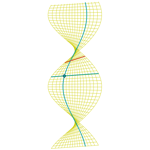 Helicoide
Helicoide
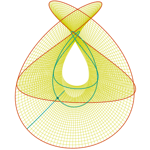 Henneberg
Henneberg
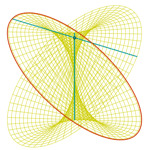
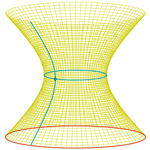 Hiperboloide
Hiperboloide
 Hiperboloide
Hiperboloide
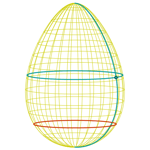 Huevo
Huevo
 Jet
Jet
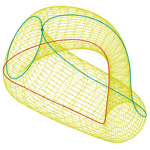 Klein
Klein
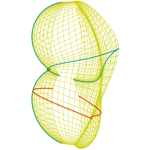 Kuen
Kuen
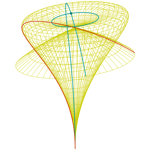 Lágrima triaxial
Lágrima triaxial
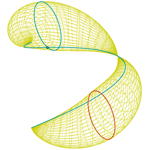 Luna creciente
Luna creciente
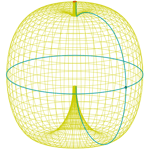 Manzana 1
Manzana 1
 Manzana 2
Manzana 2
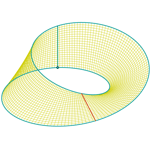 Möbius
Möbius
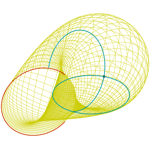 Möbius circular
Möbius circular
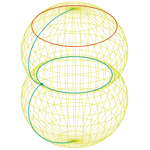 Nefroide
Nefroide
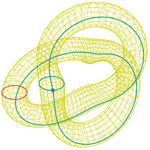 Nudo trifolio
Nudo trifolio
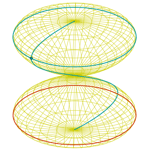 Ocho
Ocho
 Octaedro hiperbólico
Octaedro hiperbólico
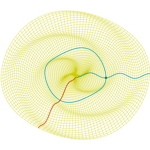 Onda espiral
Onda espiral
 Ondas
Ondas
 Papelera
Papelera
 Paraboloide
Paraboloide
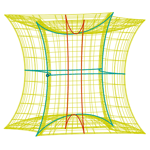
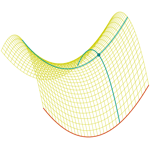 Paraboloide hiperbólico
Paraboloide hiperbólico
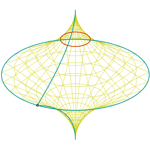 Peonza
Peonza
 Pez
Pez
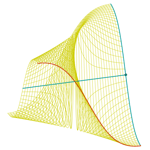 Plücker
Plücker
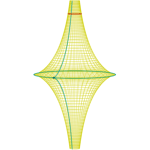 Pseudoesfera
Pseudoesfera
 Regladas
Regladas
 Revolución
Revolución
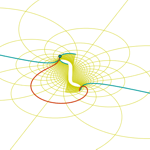 Richmond
Richmond
 Romana
Romana
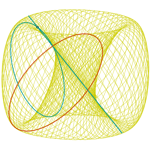 Seno
Seno
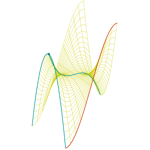 Silla de mono
Silla de mono
 Sombrero de Sherlock
Sombrero de Sherlock
 Toro
Toro
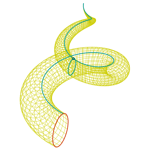 Toro espiral helicoidal
Toro espiral helicoidal
 Toro helicoidal
Toro helicoidal
 Toro umbilical
Toro umbilical
 Trompeta de Gabriel
Trompeta de Gabriel
 Wallis
Wallis
 Whitney
Whitney
 Zindler
Zindler