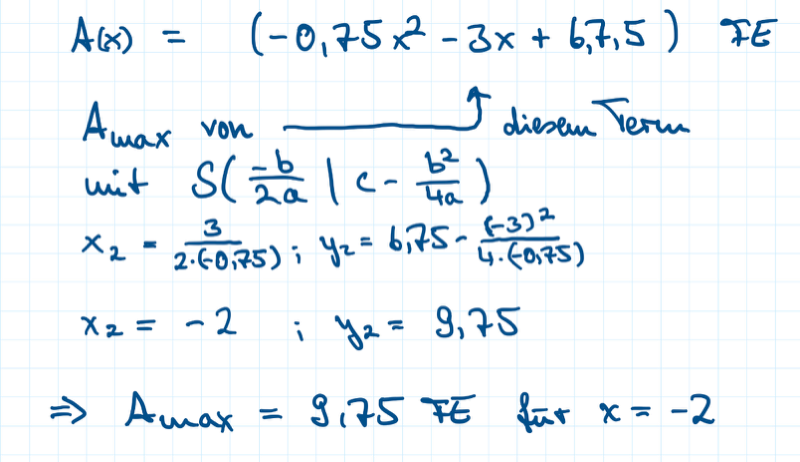Übung zu "funktionale Abhängigkeiten"
Auf der Parabel p mit der Gleichung y = – 0,5x² – 2x + 1,5 liegen die Punkte An(x|– 0,5x²– 2x+1,5) und Cn.
Dabei ist die Abszisse x der Punkte Cn stets um 3 größer als die Abszisse x der Punkte An.
a) Bestätige rechnerisch, dass für die Koordinaten der Punkte Cn in Abhängigkeit von der Abszisse x gilt:
Cn(x+3| – 0,5x²– 5x-9)
b) Die Punkte Bn(x|–3) besitzen die selbe Abszisse x wie die Punkte An. Es entstehen Dreiecke AnBnCn. Bestimme den Flächeninhalt A1 des Dreiecks A1B1C1 für x=–3.
c) Bestätige durch Rechnung, dass für den Flächeninhalt A(x) der Dreiecke AnBnCn in Abhängigkeit von x gilt:
A(x) = (– 0,75x² – 3x + 6,75) FE
d) Unter den Dreiecken AnBnCn gibt es ein Dreieck A2B2C2 mit maximalem Flächeninhalt Amax.
Berechne den maximalen Flächeninhalt Amax, sowie den zugehörigen Wert für x.
Lösung a)
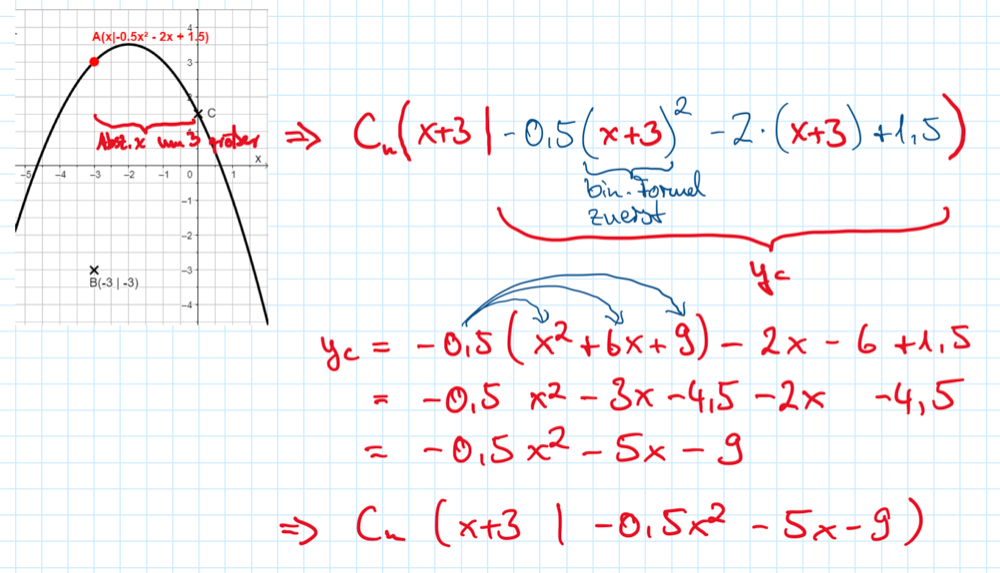
Lösung b)
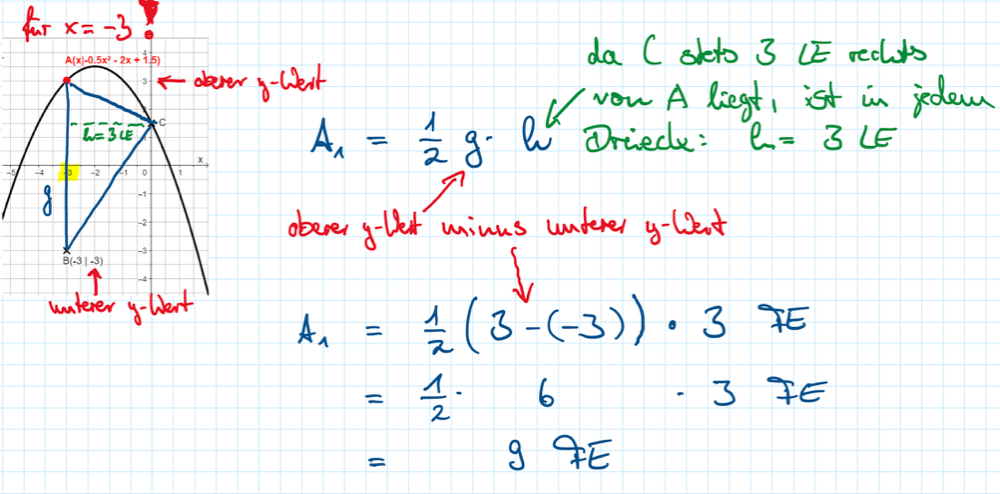
Lösung c)
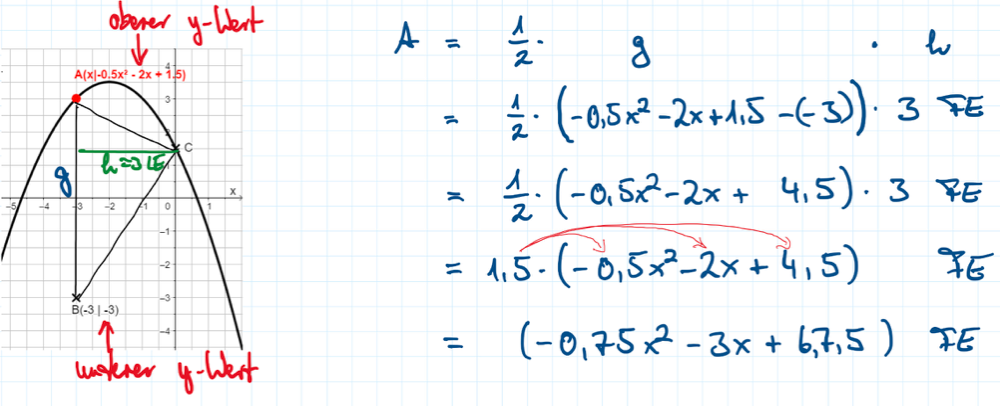
Lösung d)