Hochpunkt, Tiefpunkt oder Sattelpunkt?
Einleitung und Anleitung für die Bearbeitung des Arbeitsblattes:
Einleitung und Ausgangsfrage: In diesem Arbeitsblatt geht ihr der Frage nach, wie Hoch- und Tiefpunkte, auch Extrempunkte genannt, einer ganzrationalen Funktion rechnerisch ermittelt werden können und wie man rein rechnerisch beurteilen kann, ob es sich um einen Hoch- oder Tiefpunkt handelt. Ein weiterer besonderer Punkt mit dem man im Zuge dieser Frage unweigerlich konfrontiert wird, ist der sogenannte Sattelpunkt. Ihr werden im Zuge des Arbeitsblattes auch lernen, was es mit diesem Punkt auf sich hat. Anleitung: Geht das Arbeitsblatt schrittweise von oben nach unten durch. Sprich: Scrollt zu Beginn nicht einfach nach unten!
Bevor es richtig los geht (Startbedingungen):
Bestimmt jeweils die korrekte Ableitungsfunktion zur gegebenen Bestandsfunktion
Jetzt zurück zur Ausgangsfrage!
Schritt 1: Erinnert ihr euch noch daran, was eine Besonderheit an Hoch- und Tiefpunkten ist?!
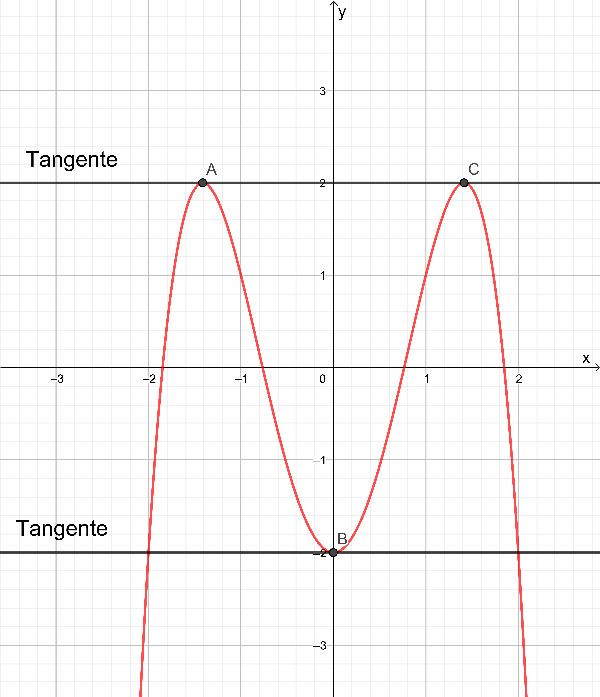
Abbildung 1
Aufgabe 1:
Benennt, wie viele Extrempunkte die betrachtete Funktion in Abbildung 1 aufweist. Benennt weiterhin wie viele Hochpunkte und wie viele Tiefpunkte darunter enthalten sind.
Aufgabe 2:
Benennt, welche Steigung die angelegten Tangenten an den jeweiligen Extrempunkten haben und erläutert kurz den Zusammenhang zwischen Tangentensteigung und Ableitung.
Aufgabe 3:
Benennt, welchen Wert die Ableitung an Extrempunkten annimmt und formuliert in Form einer Gleichung eine Bedingung für den Wert der Ableitung an Extrempunkten.
Schritt 2: Mit Kenntnis über die notwendige Bedingung für die Berechnung von Extrempunkten zurück zum Ausgangsbeispiel
Aufgabe 4:
Bestimmt zunächst die erste Ableitung von f(x).
Aufgabe 5:
Bestimmt mit Hilfe der notwendigen Bedingung alle x-Werte, an denen potentiell ein Extrempunkt vorliegen könnte. (Nach Aufstellen der Gleichung könnt ihr den GTR nutzen)
Schritt 3: Jetzt muss nur noch geklärt werden, ob an diesen Stellen tatsächlich Extrempunkte vorliegen und welche Art von Extrempunkt dies jeweils ist
Abbildung 2
Aufgabe 6:
Beschreibt mit Hilfe von Abbildung 2 wie sich die Ableitungsfunktion (durch Häkchen aktivieren) in der Umgebung des eingezeichneten Tiefpunktes (links und rechts daneben) verhält. Was geschieht dabei mit dem Wert der Ableitung?
Aufgabe 7:
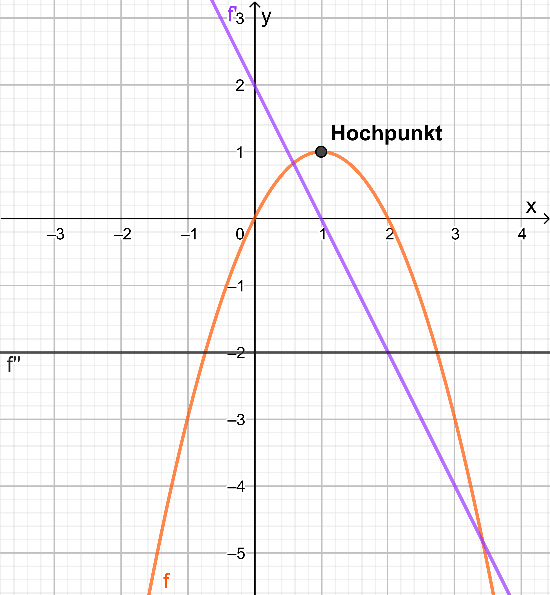
Beschreibt mit Hilfe von Abbildung 3 wie sich der Wert der Ableitung in der direkten Umgebung eines Hochpunktes verhält.
Abbildung 3
Aufgabe 8:
Formuliert mit Hilfe Ihres Wissen über den Vorzeichenwechsel der Ableitung in der Umgebung von Extrempunkten eine Regel / ein Kriterium zur Beurteilung, ob es sich bei einem Extrempunkt um einen Hoch- / oder einen Tiefpunkt handelt.
Aufgabe 9:
Erläutert anhand von Abbildung 4 was man unter einem Sattelpunkt versteht und erklärt, was hier bezüglich des Vorzeichens der Ableitung zu beachten ist (Ist das Vorzeichenwechselkriterium für einen Sattelpunkt erfüllt?)
Abbildung 4
Aufgabe 10:
Wieder zurück zum Ausgangsproblem: Beurteilt nun mit Hilfe des Vorzeichenwechselkriteriums für welchen der über die notwendige Bedingung ermittelten x-Werte ein Hoch-, Tief- oder Sattelpunkt vorliegt. Für x-Werte siehe Lösung Aufgabe 5!
Aufgabe 11:
Da die Ausgangsfrage auf Extrempunkte (und Sattelpunkte) bezogen war, müssen noch die y-Koordinaten der jeweiligen Punkte ermittelt werden. Berechnet für die ermittelten Hoch-, Tief- und Sattelpunkte die dazugehörigen y-Werte und gebt die entsprechende Punkte vollständig an.
