Voorbeeld + opgaven 3 en 4
Voorbeeld 1
Bekijk de grafiek van functie y = f(x) op het interval [0,6].
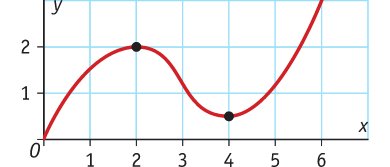
Beschrijf de veranderingen in deze grafiek.
Antwoord:
De veranderingen van deze grafiek kun je zo beschrijven:
- de grafiek is afnemend stijgend op het interval <0,2>;
- de grafiek is toenemend dalend op het interval <2,3>;
- de grafiek is afnemend dalend op het interval <3,4>;
- de grafiek is toenemend stijgend op het interval <4,6>.
- een maximum van 2 voor x = 2 : max. f(2) = 2;
- een minimum van 0,6 voor x = 4 : min. f(4) = 0,5.
Opgave 3
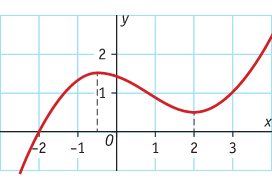
Bekijk de grafiek.
a. Beschrijf de soorten stijging en daling van de grafiek.
b. Schrijf de waarde van het lokale minimum op.
Opgave 4
Teken een grafiek die aan de volgende eisen voldoet:
- op het interval <←,-2> is er sprake van afnemende stijging
- op het interval <-2,2> is er sprake van toenemende daling
- op het interval <2,6> is er sprake van afnemende daling
- op het interval <6,→> is er sprake van constante stijging