Interpolacion Cuadratica
En numerosos fenómenos de la naturaleza observamos una cierta regularidad en la forma de producirse, esto nos permite sacar conclusiones de la marcha de un fenómeno en situaciones que no hemos medido directamente.
La interpolación consiste en hallar un dato dentro de un intervalo en el que conocemos los valores en los extremos.
La interpolación cuadrática. Fórmula de Lagrange
Cuando el polinomio que conviene es de 2º grado la interpolación recibe el nombre de cuadrática. El polinomio interpolador es único, luego como se encuentre da igual., sin embargo, a veces los cálculos son muy laboriosos y es preferible utilizar un método que otro. A la vista de los datos se decide.
podemos utilizar la expresión del polinomio interpolador así:
y= a + b(x-x0) + c(x-x0)(x-x1), con lo que la búsqueda de los coeficientes es muy sencilla.
Lagrange (1736-1813) dio una manera simplificada de calcular los polinomios interpoladores de grado n Para el caso de un polinomio de 2º grado que pasa por los puntos (x0, y0 ), (x1, y1), (x2, y2):
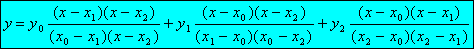 la cual es la fórmula de Lagrange para n=2.
la cual es la fórmula de Lagrange para n=2.
EJERCICIOS PROPUESTOS
1. El número de turistas que visitaron España en el periodo 1975-1990 está reflejado en la siguiente tabla:
Calcular, utilizando un polinomio de interpolación adecuado (cuadrático, al menos), el número de turistas que visitarán España en 1995.
2. En la tabla siguiente se indica el tiempo (en días) y el peso (en gramos) de tres embriones de cierta especie animal:
a) Obtener el polinomio de interpolación de 2º grado correspondiente.
3) Obtener la ecuación de la interpolación cuadrática que pasa por los puntos A(0,4), B(1,3) y C(-1, 9).
| Años | 1975 | 1980 | 1985 | 1990 |
| Millones de turistas | 24,1 | 30,1 | 38,1 | 43,2 |
| Tiempo | 3 | 5 | 8 |
| Peso | 8 | 22 | 73 |