Cercle inscrit dans un triangle
Tâche
Construire un cercle inscrit dans un triangle.
D'abord, explorez la construction ci-dessous. Ensuite, apprenez à la construire à votre tour avec l'application Géométrie de la Calculatrice Suite de GeoGebra en suivant les instructions un peu plus bas sur cette page.
Explorez cette construction. Bougez les sommets du triangle et observez le cercle inscrit.
Instructions
Remarque: Si vous utilisez l'application mobile, assurez-vous que l'option d'étiquetage choisie est "Tous les nouveaux points". Accédez aux propriétés dans le menu de l'application puis sélectionnez les propriétés Globales.
| 1. | 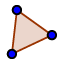 | Affichez la fenêtre Outils. Créez un triangle ABC avec l'outil Polygone. |
| 2. | 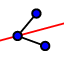 | Sélectionnez l'outil Bissectrice et créez la bissectrice de deux angles du triangle. Conseil: En sélectionnant dans l'ordre les sommets A, B puis C, c'est la bissectrice de l'angle B qui sera créée. |
| 3. |  | Créez le point d'intersection D des deux bissectrices avec l'outil Intersection. |
| 4. | 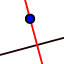 | Sélectionnez l'outil Perpendiculaire et créez une perpendiculaire à un côté du triangle passant par le point D. |
| 5. |  | Sélectionnez à nouveau l'outil Intersection et créez le point E à l'intersection du côté choisi et de sa perpendiculaire. |
| 6. | 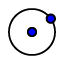 | Sélectionnez l'outil Cercle (centre-point) et créez un cercle de centre D, passant par le point E. |
| 7. |  | Masquez les lignes auxiliaires utilisées pour la construction. |
| 8. |  | Avec l'outil Segment, reliez les points D et E pour afficher le rayon du cercle inscrit. |
| 9. |  | Affichez l'angle droit entre le rayon du cercle inscrit et le côté du triangle avec l'outil Angle. |
| 10. |  | Sélectionnez l'outil Déplacer et bougez les sommets du triangle. Vous devriez observer que le cercle reste toujours inscrit au triangle. |