Circle as an implicit equation in polar form

The general polar equation of a circle of radius

centered at

. This equation is derived from the Law of Cosines. Using that

and

we can transform this polar equation to a cartesian one:

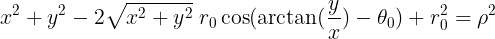
Instead of the

we use atan2(y,x) in GeoGebra, as this function gives us an angle in [0,360)

Another possibility is to use the general circle equation in cartesian form

and substitute

and

so we get

as the implicit equation.

New Resources