matchingを安定させよう
1.マッチング
このワークシートはMath by Codeの一部です。
2部グラフはグラフGが2種の頂点群VA,VBに分割できて、
辺がどれもVAとVBにまたがるものだけというものだったね。
G(VA,VB,E)と表示しました。
<カップル問題>
ここで2部グラフにかかわる問題で、うまくカップル、ペアを作ること(結婚問題)だ。
質問:n人の女とそれと同数以上のm人の男がいる。どの女にも何人か男の知り合いがいる
すべての女が知り合いの男とカップルになれる必要条件は何でしょう。
たとえば、VAの点が女、VBの点が男として、知り合いをすでにある辺としよう。
男と女はカップルにならないから、男と女の2部のグラフであることがまず必要だ
すると、一人の男だけが知り合いとして集中してしまうとカップルは作れない。
知り合いがバラけていないとカップルがうまくさがせないね。
うまくカップルを作った状態、辺の選択をマッチングという。
マッチングMはどの2つの辺も同じ頂点に接続しないことと、
Mは2部グラフのE(G)の部分集合になることが必要だ。
<Hallの定理>
この知り合いがバラけているというのを数式にした人がいる。それがHallさん。
VAの部分集合U(何人かの女)をどう選んでも、
それらに隣接する点(知り合いの男)、N(U)は数の上で同数以上であることが必要十分だ。
つまり、任意の |N(U)| ≧ |U|。
鳩の巣原理の反対だね。
狭まると被るが必ずあるから、被らずに選べるためには同じ以上に広げないとね。
<最大マッチング>
完全2部グラフKn,mのマッチングMの辺集合をPとしよう。Pの要素である辺はそれぞれ接続していない。
だから、Kn,mの辺の集合Eに対する、Pの補集合をQとしたときに、Pの要素とQの要素を交互につなぐことで、折れ線ができるね。
この折れ線の両端がPの要素の場合はマッチングが最大化しているけれど、折れ線の両端がQの要素になっている場合は、一斉にPとQの要素を入れ替えると、辺の数を増加できる。そして、マッチング数が1増やせる。こうやって、マッチングを最大化することができるね。
<完全マッチング>
さきのカップル問題では男は女よりも同数以上だったから、男が女より多い場合女から見れば
無事に全員カップルができるが、男が余ってしまう。
男女を同数にすると余るなくカップルができる。これが完全マッチングだ。
つまり、|VA|=|VB|=nで、マッチングMの辺の数もnになる。
2.安定マッチング
マッチングにしても、完全マッチングにしても
ペアが作れることと、ペアが安定していることは別の問題だ。
好みの順位というものがあると、ペアができても不満、不安定さが残ることがありうる。
好みが高い順に異性の名前をリストにしたとしよう。
男を小文字、女を大文字で表すとして、男の部の頂点がVm=[a,b,c],女の部の頂点がVW=[A,B,C]
だから、2部グラフG(Vm,VW,E)の|E|は3*3=9本の辺だね。
a=[A,B,C], b=[B,A,C],c=[A,C,B]
A=[b,a,c], B=[c,b,a], C=[a,c,b]とする。
この場合のマッチングMはEの部分集合で3辺になる。
M1=[(a,B),(b,C),(c,A)] よりもM2=[(a,A),(b,B),(c,C)]の方が安定している。なぜなら、
・M1はa->Bは2位だが、B->aは3位。b->Cは3位でC->bも3位。c->Aは1位でもA->cは3位。
女は3人とも3位の男とのペアになっている。
・M2はa->Aは1位で、A->aは2位。b->Bは1位でB->bは2位。c→Cは2位でC→cは2位。
男はA,Bが1位の女とのペアで、他の人も全部2位とのペアになっている。
安定マッチング(stable matching)と言えるのは両方ともさらに高い順位になるペアmWがないものだ。
だから、M2は安定マッチングといえる。
質問:安定マッチングをするためにはどんな手順でやったらよいでしょうか。
どの男も、どの女も異性に好き順位表をもっているとします。
たとえば、男が順に女にプロポーズします。女は先約がないなら受け付けます。
先約がいたら、女は順位の高い方に切替ますが、
切り替える前には、順位の低いペアになる好き順位表から相手を削除します。
切り替えたあとは、断られた男は次に好きな女にプロポーズする。
これをくり返します。
以下は、それをpythonで作ったものです。
import matplotlib.pyplot as plt
import networkx as nx
# ========= 描画作成用関数
def draw_G(Va,Vb,pertner):
G = nx.Graph()
G.add_nodes_from(Va)
G.add_nodes_from(Vb)
for k,v in pertner.items():
G.add_edge(k,v)
global pic_num
plt.subplot(2,4,pic_num)
colorList = ['Green']*len(Va) + ['Red']*len(Vb)
nx.draw_networkx(G,node_color=colorList)
pic_num +=1
return G
# ========= マッチング用関数
def propose(m):
W = prefer[m][0]
refuse(W,m)
def refuse(W,m):
print(f"プロポーズ男{m}→女{W}")
if not W in pertner:
pertner[W] = m
print('ペアができました。',pertner)
draw_G(Vm,VW,pertner)
else:
m_dash= pertner[W]
if prefer[W].index(m) > prefer[W].index(m_dash):
#男mのWへのプロポーズを拒否する
prefer[W].remove(m)
prefer[m].remove(W)
print(f"女{W}は{m}を拒否し、男{m}は{W}をあきらめる。")
propose(m)
else:
#男mのWへのプロポーズを受け入れる
print('ペアの変更です。',pertner)
pertner[W] = m
draw_G(Vm,VW,pertner)
prefer[W].remove(m_dash)
prefer[m_dash].remove(W)
print(f"女{W}は{m}を受け入れて{m_dash}を捨てる。男{m_dash}は{W}をあきらめる。")
propose(m_dash)
def stableMatch():
for man in Vm:
propose(man)
return pertner
#2部グラフのデータ
Vm=['a','b','c']
VW=['A','B','C']
E=[]
# マッチング用の好き順位の辞書とパートナーの実況データ
prefer={'a':['A','B','C'], 'b':['B','A','C'],'c':['A','C','B'],'A':['b','a','c'], 'B':['c','b','a'],'C':['a','c','b']}
pertner={}
pic_num = 1
# 実行はこれだけ
stableMatch()
#===============================
[OUT]
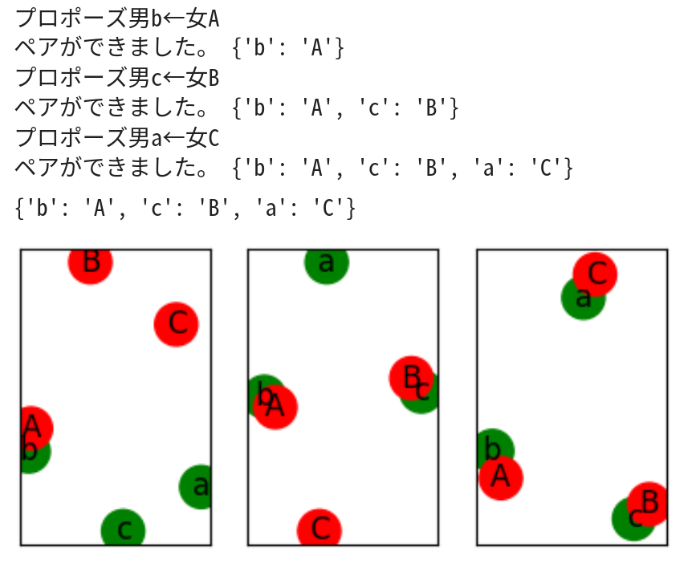
プロポーズ男a→女A
ペアができました。 {'A': 'a'}
プロポーズ男b→女B
ペアができました。 {'A': 'a', 'B': 'b'}
プロポーズ男c→女A
女Aはcを拒否し、男cはAをあきらめる。
プロポーズ男c→女C
ペアができました。 {'A': 'a', 'B': 'b', 'C': 'c'}
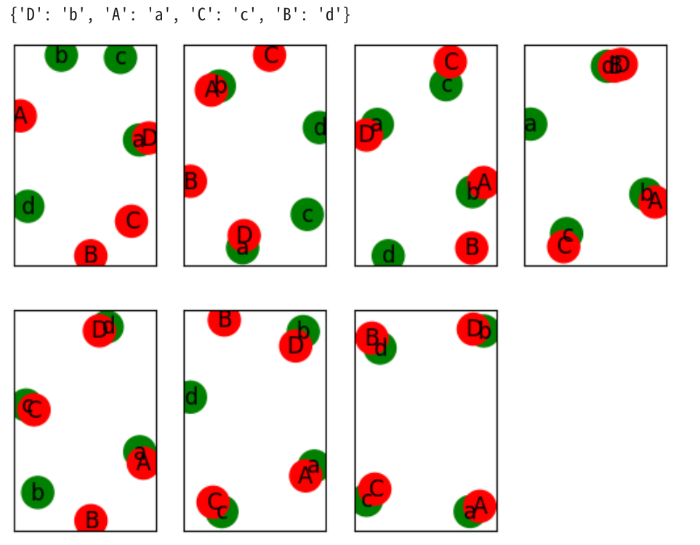
4人ずつの男女で、もう少し手間取りそうなものをやってみよう。
#2部グラフのデータ
Vm=['a','b','c','d']
VW=['A','B','C','D']
E=[]
# マッチング用の好き順位の辞書とパートナーの実況データ
prefer={'a':['D','A','C','B'], 'b':['A','C','D','B'],'c':['C','D','B','A'],'d':['D','A','C','B'],
'A':['a','c','d','b'], 'B':['d','a','b','c'],'C':['c','b','d','a'],'D':['b','d','c','a']}
pertner={}
pic_num = 1
# 実行はこれだけ
stableMatch()
#===============================
[OUT]
プロポーズ男a→女D
ペアができました。 {'D': 'a'}
プロポーズ男b→女A
ペアができました。 {'D': 'a', 'A': 'b'}
プロポーズ男c→女C
ペアができました。 {'D': 'a', 'A': 'b', 'C': 'c'}
プロポーズ男d→女D
ペアの変更です {'D': 'a', 'A': 'b', 'C': 'c'}
女Dはdを受け入れてaを捨てる。男aはDをあきらめる。
プロポーズ男a→女A
ペアの変更です {'D': 'd', 'A': 'b', 'C': 'c'}
女Aはaを受け入れてbを捨てる。男bはAをあきらめる。
プロポーズ男b→女C
女Cはbを拒否し、男bはCをあきらめる。
プロポーズ男b→女D
ペアの変更です {'D': 'd', 'A': 'a', 'C': 'c'}
女Dはbを受け入れてdを捨てる。男dはDをあきらめる。
プロポーズ男d→女A
女Aはdを拒否し、男dはAをあきらめる。
プロポーズ男d→女C
女Cはdを拒否し、男dはCをあきらめる。
プロポーズ男d→女B
ペアができました。 {'D': 'b', 'A': 'a', 'C': 'c', 'B': 'd'}
好み順位表に対してマッチングの安定感はどうなのだろうか?
男がプロポーズするというしくみだから、男の方が女にとってよりもよい結果になったと思われる。
prefer={'a':['D','A','C','B'], 'b':['A','C','D','B'],'c':['C','D','B','A'],'d':['D','A','C','B'],
'A':['a','c','d','b'], 'B':['d','a','b','c'],'C':['c','b','d','a'],'D':['b','d','c','a']}
{'D': 'b', 'A': 'a', 'C': 'c', 'B': 'd'}
AaペアはAの1位、aの2位。男女ともに順位が高い。BdペアはBの1位、dの1位。
CcペアはCの1位、cの1位。DbペアはDの1位、bの3位。
あれっ?そうでもなさそうだね。
女にとってはすべて1位の相手になった。
女が選ぶ、プロポーズするというしくみにたらどうなるのだろうか。
質問:コードをどう変えると女がプロポーズするpropose,refuse,stableMatch関数になるでしょうか。
コードを作り変えて実行してみると、結果は。。。
#========================================
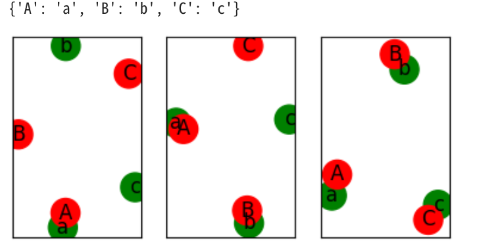
プロポーズ男a←女A
ペアができました。 {'a': 'A'}
プロポーズ男d←女B
ペアができました。 {'a': 'A', 'd': 'B'}
プロポーズ男c←女C
ペアができました。 {'a': 'A', 'd': 'B', 'c': 'C'}
プロポーズ男b←女D
ペアができました。 {'a': 'A', 'd': 'B', 'c': 'C', 'b': 'D'}
すんなりとマッチングが完了します。
{'D': 'b', 'A': 'a', 'C': 'c', 'B': 'd'}だったのが、{'a': 'A', 'd': 'B', 'c': 'C', 'b': 'D'}に変わった。
ペアができる順番は変わったが結果はまったく同じになった。
このマッチングはかなりよくできているのかもしれない。