Ecuación general de segundo grado
Contenido
- Ecuación general cuando
- Ecuación general cuando
- Discriminante de las cónicas
La ecuación general de segundo grado, también llamada ecuación de las cónicas, es de la forma . El término es llamado término rectangular.
Cuando el término rectangular es nulo (B = 0), el eje focal de la cónica es paralelo a uno de los ejes coordenados.
Cuando el término rectangular no es nulo (), el eje focal de la cónica no es paralelo a uno de los ejes coordenados sino que sufre una rotación con relación a ellos.
Discriminante de las cónicas
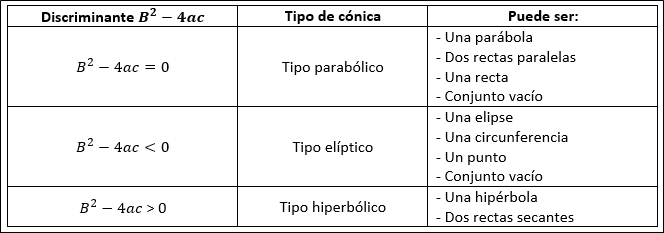
Discriminante es la expresión . Su resultado indica el tipo de cónica como se detalla en la siguiente tabla.
No siempre la ecuación general de segundo grado define una parábola, una elipse, una circunferencia o una hipérbola. Se presentan casos especiales dependiendo de los valores de los coeficientes de la ecuación:
- Cuando el discriminante es cero se puede tener parábola, dos rectas paralelas, una recta o conjunto vacío.
- Cuando el discriminante es menor que cero se puede tener elipse, circunferencia, un punto o conjunto vacío.
- Cuando el discriminante es mayor que cero se puede tener hipérbola o dos rectas secantes.
Ecuación general de segundo grado cuando B = 0
Cuando B = 0, el discriminante quede reducido a la expresión - 4AC. Se presentan tres casos:
1. . La ecuación es de tipo parabólico cuando A o C o las dos sean iguales a cero.
2. . La ecuación es de tipo elíptico cuando A y C son de igual signo (los dos coeficientes negativos o los dos positivos).
3. . La ecuación es de tipo hiperbólico cuando A y C son de signos contrarios.
El applet que se presenta permite mostrar los diferentes casos cuando en la ecuación general B = 0.
- Se puede modificar la escala: Botón Alejar, Botón Aproximar.
- Se puede mostrar información adicional a cada ecuación definida: Botón Sí, Botón No.
Explore ejemplos que cumplan cada una de las siguientes condiciones. Analice el valor del discriminante y la información que se presenta:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)
n)
o)
p)
Ecuación general de segundo grado
Como ya se indicó, cuando el término rectangular es nulo (B = 0), el eje focal de la cónica es paralelo a uno de los dos ejes coordenados, mientras que si , el eje focal queda rotado. Esto se puede visualizar en el segundo applet.
Para obtener un ejemplo de ecuación de tipo parabólico, buscar valores de B, A, C que cumplan que . Por ejemplo, B = 4, A = 2, C = 2 o B = 4, A = 1, C = 4.