Öklid bağıntıları'in kopyası

Matematikteiki doğru veya iki düzlem (veya bir doğru ve bir düzlem) kesiştiklerinde oluşturdukları komşu açılar birbirine eşitse dik olarak kabul edilir.

İç açılardan birinin 90 derece olan üçgene dik açılı üçgen denir.

İki üçgenin karşılıklı ikişer açıları eş ise bu üçgenler benzerdir. Benzerlik oranı olarak ise; eşit açıların karşısındaki kenarların uzunlukları oranı yazılır.

Diklik kavram, dik üçgen ve benzerliği hatırladığımıza göre öklid teoremine geçelim Bir dik üçgende dik açının olduğu köşeden karşı kenara indirilen dikme için bazı eşitlikler tanımlanır. Şimdi bunları bulmaya çalışacağız

EAC,ECB,CAB üçgenlerinin benzer üçgenler olduğunu benzerlik konusundan biliyoruz.

EAC üçgeni ECB benzerdir. |AE| / |EC|=|EC|/ |EB| eşitliği kullanarak nasıl bir bağıntı elde edebilirsiniz ?

EAC ile CAB üçgenleri benzerdir. O halde |AC|/|AB|=|AE|/|AC| eşitliğini kullanarak nasıl bir bağıntı elde edebilirsiniz ?

ECB ile CAB üçgenleri benzerdir. O halde |CB|/|AB|=|EB|/|CB| eşitliğini kullanarak nasıl bir bağıntı elde edebilirsiniz?

Sürgüden CBA açısının değerini değiştirin ve ne gözlemlediğinizi yazınız.

bulduğunuz bağıntıda h(yükseklik) ile p yada k arasında bir ilişki var mıdır ? Yüksekliğimiz artarsa p ve k için ne söylenebilir ?

applet üzerinde ACB üçgeninin h,p,k,a ve b kenarlarının uzunluklarını hesaplayınız. sürgümüzdeki değer yardımıyla kenar uzunluklarımızı değiştirdikçe bulduğunuz bağıntının hala geçerli mi olup olmadığını inceleyiniz.

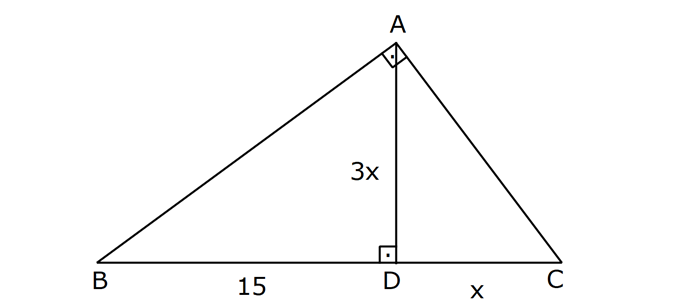
yukarıdaki dik üçgende verilen x uzunluğunu nedir ?

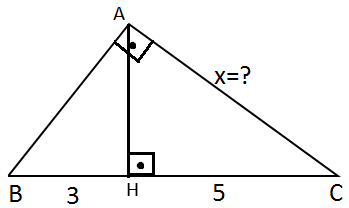
Yukarıdaki şekilde verilen x uzunluğunu hesaplayınız.

Öklid bağıntıları'in kopyası

New Resources

Discover Resources

Discover Topics