Resolução dos exercícios
1-
a)
Solução:
Sabendo que um prisma possui 2 bases congruentes, que são as secções paralelas e distintas, então: 7-2= 5 faces laterais.
Logo, a natureza desse prisma é um prisma pentagonal.
b)
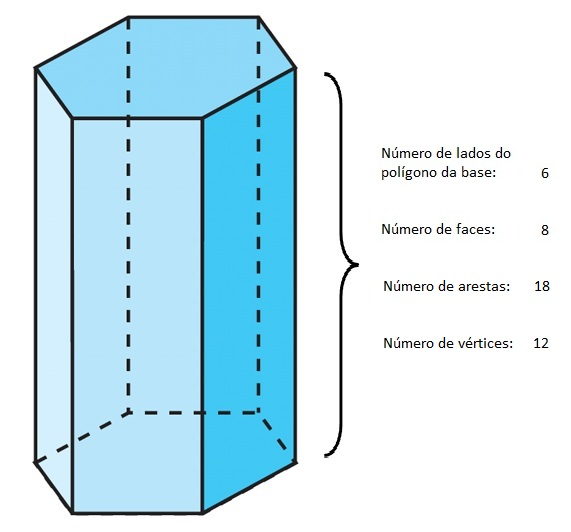
c)
Solução:
Sabendo que um prisma possui 3n arestas, logo temos: 15 arestas = 3n
Então: n= 15/3, onde n=5 arestas
Resposta: A natureza desse prisma é um prisma pentagonal
d) Prisma Octogonal
2-
Solução:
Como o prisma possui 2 bases e n faces laterais:
S=2.(n-2).2r + n.4r
S=n.4r-8r + n.4r
S=n.8r - 8r
S=(n-1).8r
Logo:
S=(n-1).8.r
72.90=(n-1)8.90
6480=720n - 720
n= 7200/720
n=10
Logo, sua natureza é um prisma decagonal.
3-
S= n.8r - 8r
S= (n-1).8r
32.90=(n-1)8.90
2880=720n - 720
n=3600/720
n=5
Logo, sua natureza é um prisma pentagonal
4-
Para calcular a soma dos ângulos internos de todas as faces de um prisma de n faces laterais, temos: S=(n-1).8r
No problema é um prisma oblíquo de 8 faces.Sabemos que o prisma tem 2 bases, logo o número de faces laterais do problema será 8-2= 6. Aplicando na fórmula, temos
S=(6-1).8r
S=40r
S=40.90
S=3600
5-
S=(n-1).8r
S=(5-1).8.90
S= 2880
6-
Sabendo que o lado e a altura do prisma hexagonal são respectivamente 0,3 e 1,5 cm, calculamos o volume de cada prisma hexagonal:
V= 3a²3 /2 X h
V= 3.0,3²3 /2 X 1,5
V= 0,273 /2 X 1,5
V= 0,4053 /2
V= 0,35 cm³ cada prisma hexagonal
Sabendo que o volume total do favo é 315 cm³, faremos:
315 = 0.35 . x
x= 900 prismas hexagonais
7 -
14.478.900,65 = 5 a² . tg 72º . x /4
14.478.900,65 = 5 (16.5x)² tg 72º x /4
57.915.602,6 = 4.189,496715 x³
x³ = 13.824
x = 24 m
8 -
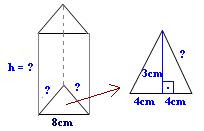
Pela relação de Pitágoras temos:
O perímetro da base vale: 5 cm + 5 cm = 8 cm = 18 cm
A altura do prisma vale 1/3 x 18 = 6 cm
Logo, área total
Ab = lado da base x altura / 2
Ab = 8 x 3 /2 = 12 cm ²
Al = lado da base x altura do prisma
Al = (8x6) + 2x(5x6) = 108 cm ²
At= 2x12 + 108
At= 132 cm²