Visualisierung des numerischen Verfahrens zur Identifizierung der Art der Extrema von Funktionen mit zwei Variablen auf einer Konturkarte (Contour Map)
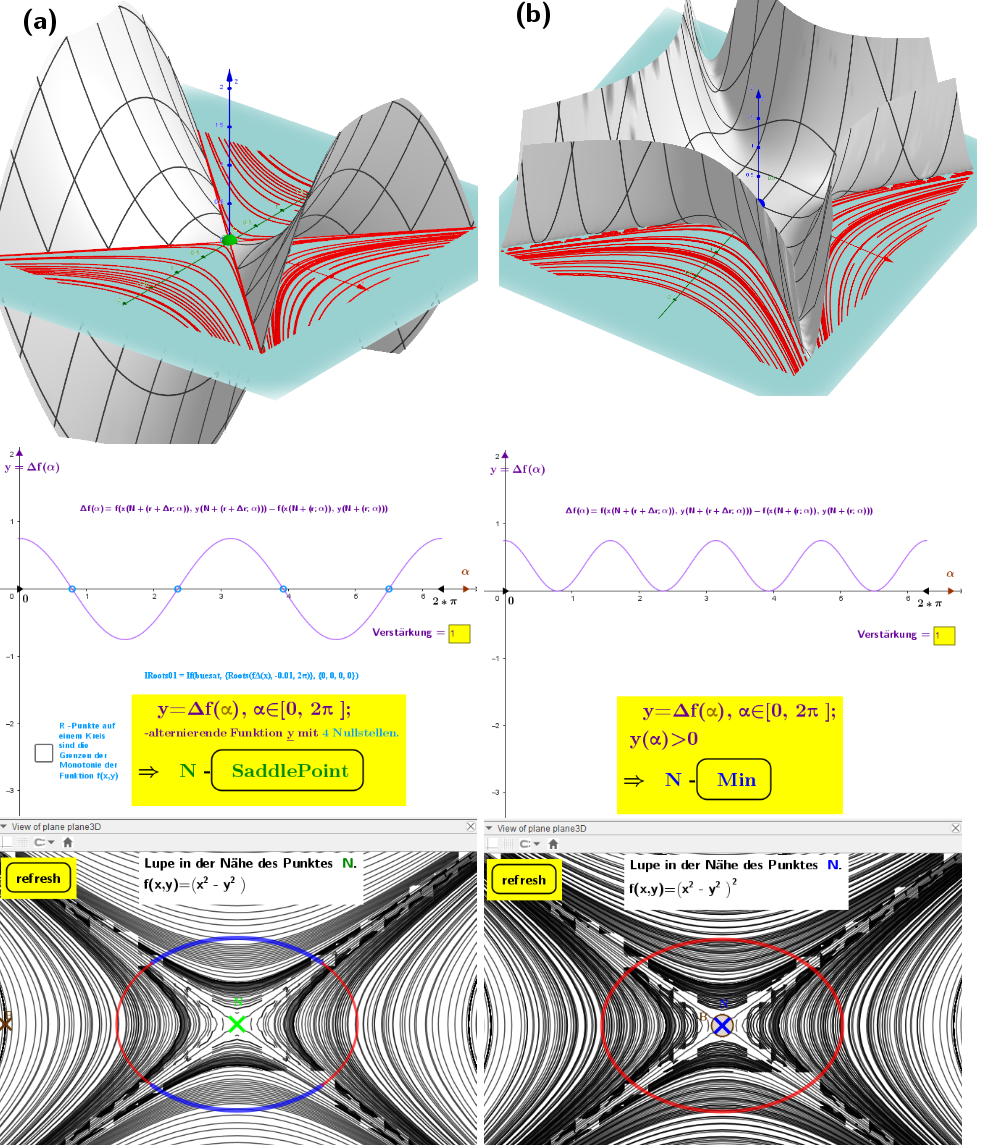
Für die Funktion f(x,y) mit zwei Variablen auf einer Konturkarte wird ein numerisches Verfahren zur Bestimmung der Art der Extrema ohne Verwendung der Ableitungen vorgeschlagen.
Die Analyse basiert auf der zusammengesetzten Funktion Δf(α) - Änderungen der Funktion f(x,y) für die entsprechenden Punkte auf den Kreisen (r; α) und (r+Δr; α). Das Applet bestimmt Bereiche monotoner Zunahme oder Abnahme für die untersuchten Funktion f(x,y) auf einem Testkreis, der um einen kritischen Punkt auf der Konturkarte beschrieben wird.
✱Wenn Δf(α)<0 für α∈[0,2 π ], dann nimmt f(x,y) an den Enden der Radien r und r+Δr der Kreise (für jedes α) ab, d.h. es gibt ein lokales Maximum in ihrem Zentrum.
✱Wenn Δf(α)>0 für α∈[0,2 π ], dann nimmt f(x,y) an den Enden der Radien r und r+Δr der Kreise (für jedes α) zu, d.h. es gibt ein lokales Minimum in ihrem Zentrum.
✱Wenn Δf(α) für α∈[0,2 π ], eine alternierende Funktion mit Nullstellen (in der Farbe „Deep Sky Blue“) ist, dann hat f(x,y) steigende und fallende Funktionsabschnitte an den Rändern dieser Kreise, d.h. es gibt einen Sattelpunkt in der Mitte dieser Kreise. In der Nähe dieses Punktes hat die Fläche die Form eines Sattels um den kritischen Punkt: - konkav nach oben in einer Richtung, - konkav nach unten in einer anderen Richtung.
 *Das Applet bietet die Möglichkeit, die Genauigkeit dieser Berechnungen zu überprüfen, indem die berechneten Monotoniegrenzen verfolgt werden (Schaltfläche "Trace On").
**Im Fall von Index=1 ist es möglich, Funktionen aus dem Eingabefeld einzugeben.
*Das Applet bietet die Möglichkeit, die Genauigkeit dieser Berechnungen zu überprüfen, indem die berechneten Monotoniegrenzen verfolgt werden (Schaltfläche "Trace On").
**Im Fall von Index=1 ist es möglich, Funktionen aus dem Eingabefeld einzugeben.
Funktionsgraphen (index=3) mit gleichem Konturdiagramm: f(x,y)=(x²-y²)ᴷ für k=1 und k=2
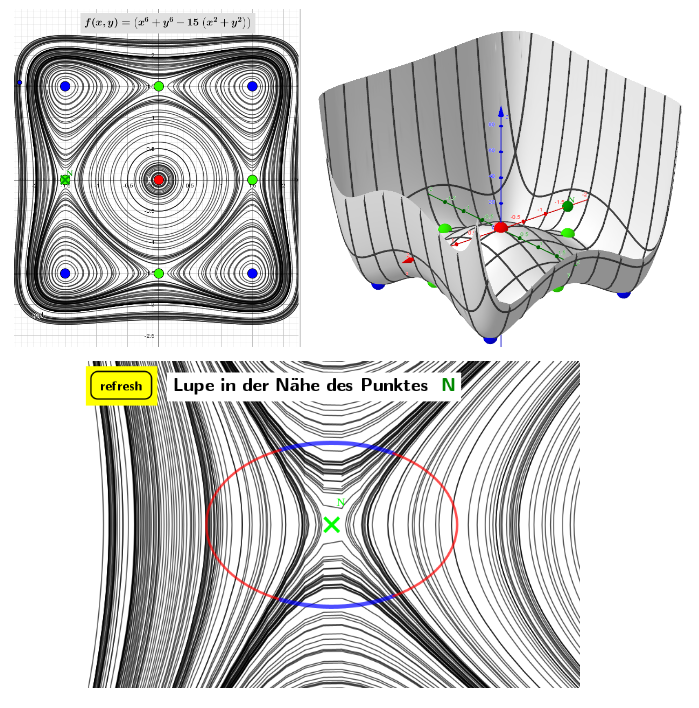
Beispiel (index=7): f(x,y)=x⁶+y⁶-15(x²+y²)
Beispiel (index=8): f(x,y)=3(1-x²) exp(-(x-0.5)²-(y+1)²)-2(0.2x-x³-y⁵)exp(-x²-y²)sin(x-y)
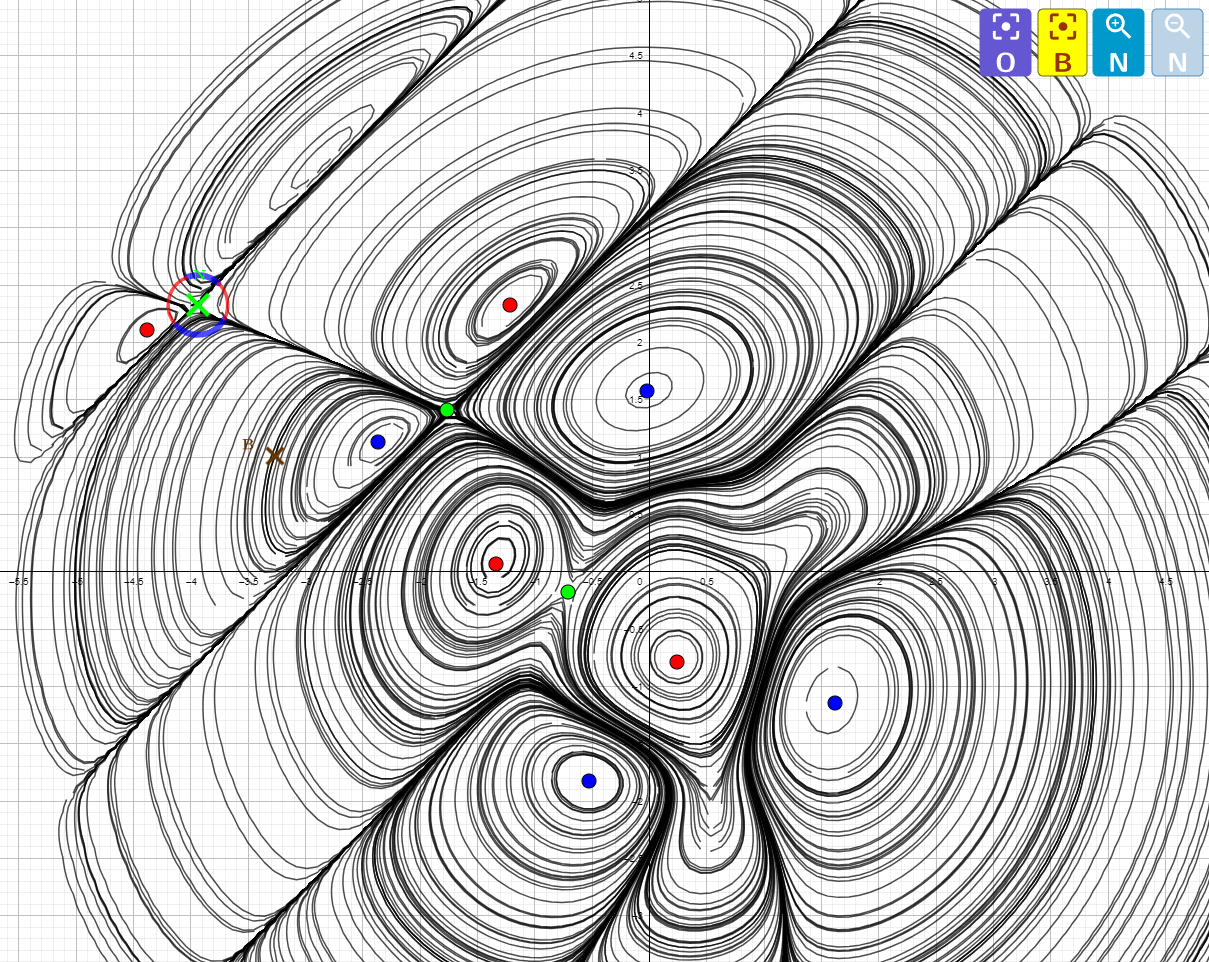
Beispiel (index=9): Ist N ein Sattelpunkt?
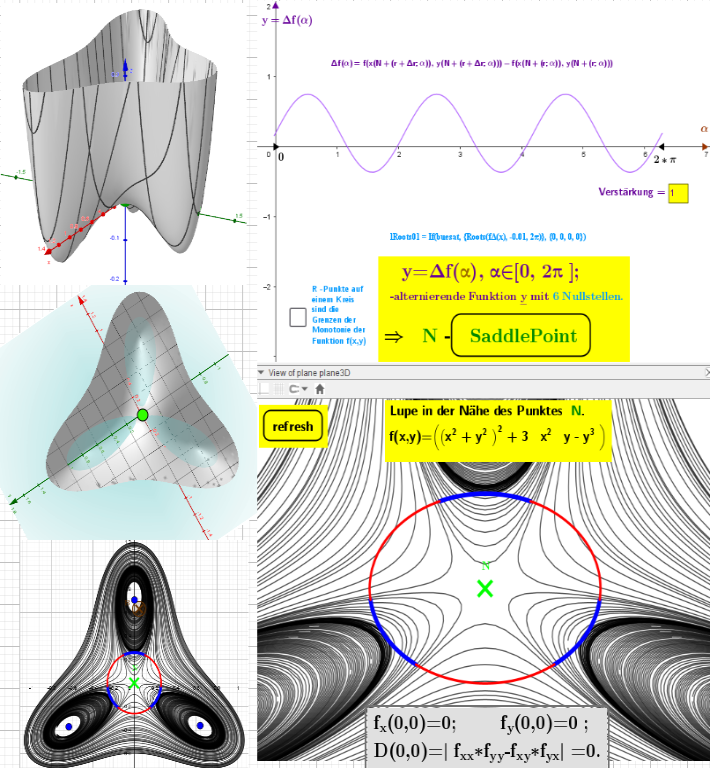
Schema zur Berechnung stationärer Punkte Funktion 2 Variablen
