Reconocer regularidades en el comportamiento de las razones trigonométricas con ángulos de 30º, 45º y 60º.

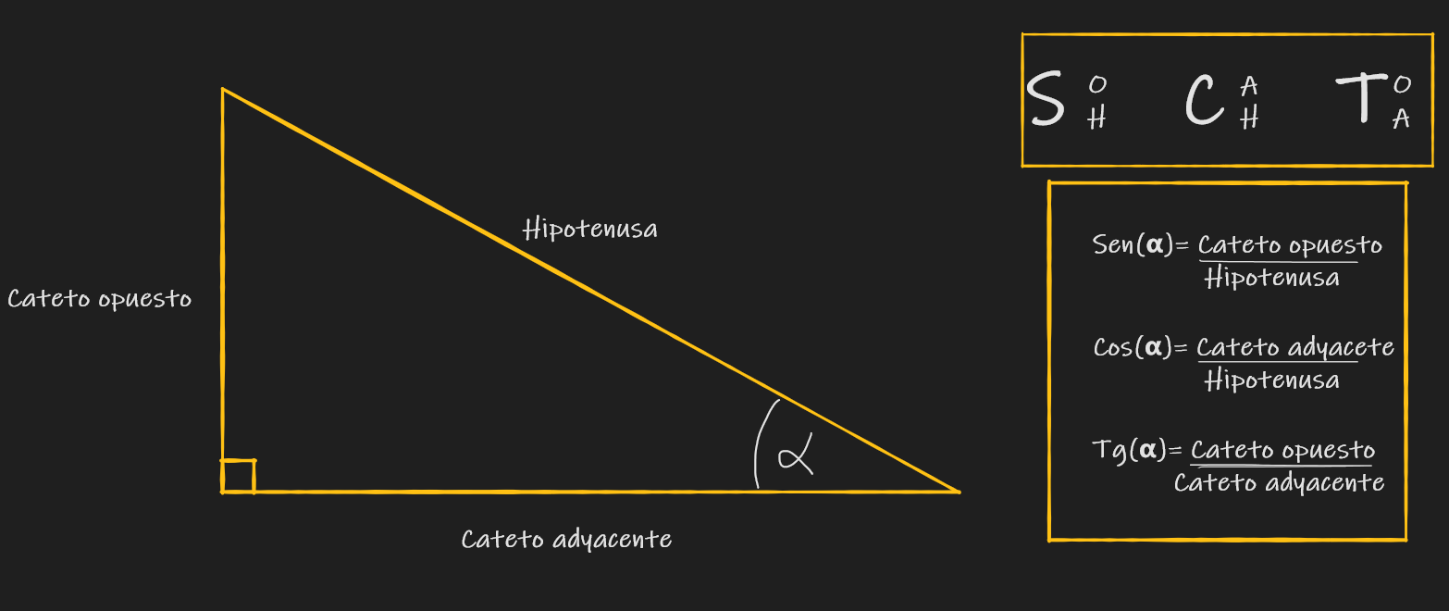
Para un valor de , ¿Cuál es el valor de la hipotenusa para el triángulo rectángulo Isósceles y Escaleno?

Para un valor de , ¿Cuál es el valor del cateto opuesto al ángulo de ?

Para un valor de ,¿Cuál es el valor del cateto adyacente al ángulo de ? (en caso de ser necesario, considera )

Andrés crea un triángulo que mide metros de altura, con una base de metros y necesita determinar uno de los ángulos interiores ( ), ayuda a Andrés y encuentra .

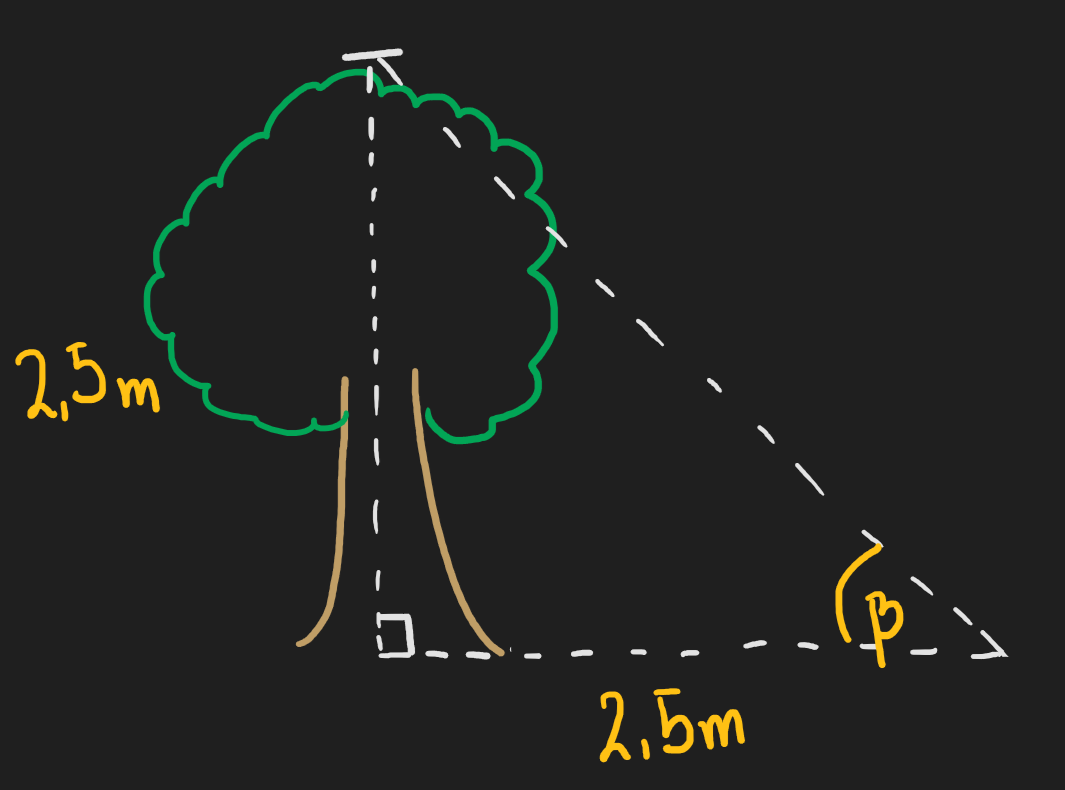
Considerando que tanto la atura y sombra proyectada de un árbol es de metros, indique la medida del ángulo

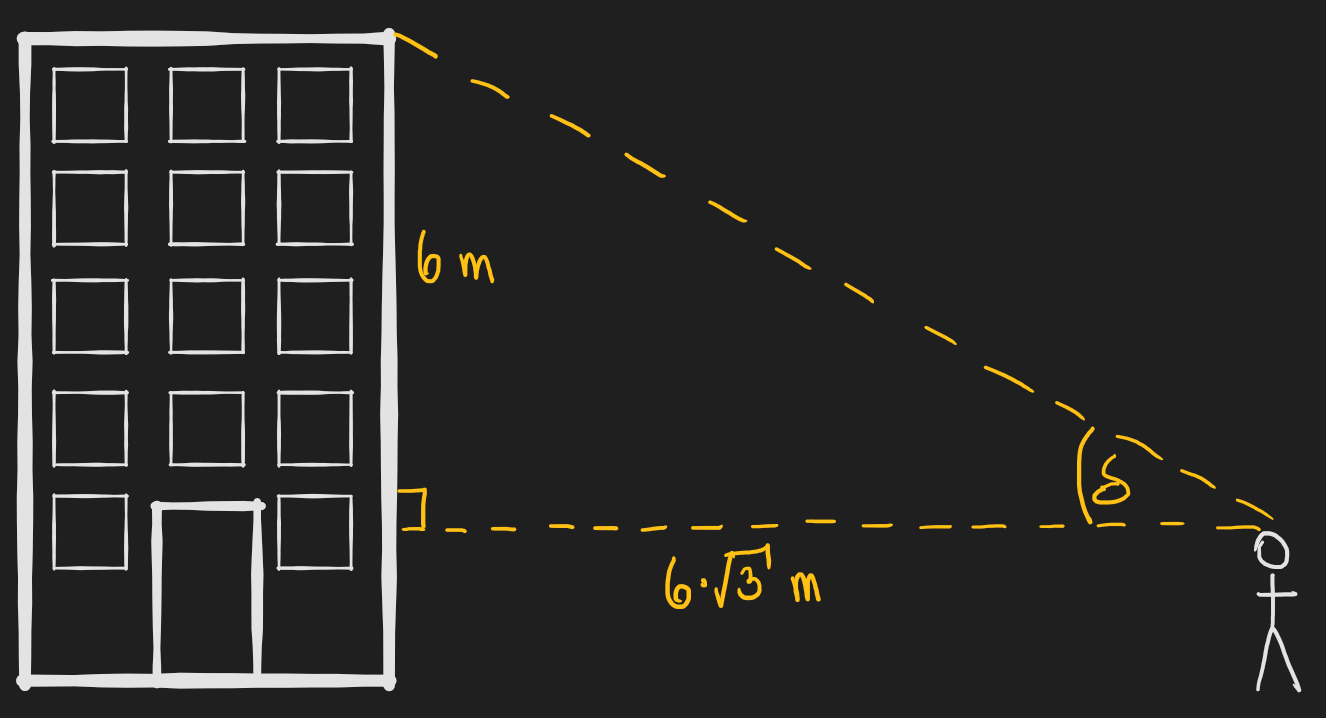
Juan observa a metros de distancia un edificio, el cual presenta un espacio para colocar un anuncio, dicho anuncio indica sus medidas donde su alto es de metros, a lo que Juan se plantea encontrar el ángulo con el que él mira lo más alto del anuncio, ¿Cuánto vale dicho ángulo ()?