Introduccion
Definición de Función
Una función es una regla de asociación que relaciona dos o mas conjuntos entre si; generalmente cuando tenemos la asociación dos conjuntos las función se define como una regla de asociación entre un conjunto llamado dominio con uno llamado codominio, también dominio e imagen respectivamente o dominio y rango. Esta regla de asociación no permite relacionar un mismo elemento del dominio con dos elementos del codominio.
Formas de representacion
La función se puede representar de tres formas:
a) Expresión algebraica
b) Tabla
c) Gráfica
Dominio y Co dominio
Se dice que el dominio de una función son todos los valores que puede tomar el conjunto del dominio y que encuentra correspondencia en el conjunto llamado codominio, generalmente cuando se habla del plano, el dominio es el intervalo de valores que están sobre el eje de las X´s y que nos generan una asociación en el eje de las Y´s.
El otro conjunto que interviene en la definición es el conjunto llamado codominio o rango de la función, en ocasiones llamado imagen, este conjunto es la gama de valores que puede tomar la función; en el caso del plano son todos los valores que puede tomar la función o valores en el eje de las Y´s.
También, cuando se grafica en el plano cartesiano se tiene una relación de dos variables, considerando como variable aquella literal que esta sujeta a los valores que puede tomar la otra.
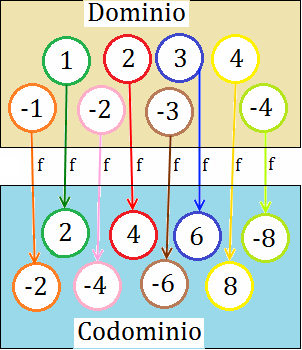 En el ejemplo, el dominio es
En el ejemplo, el dominio es
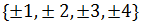 El codominio es
El codominio es
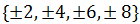 Y la exprsión de la función es
Y la exprsión de la función es
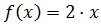 ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
 En el ejemplo, el dominio es
En el ejemplo, el dominio es
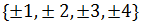 El codominio es
El codominio es
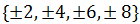 Y la exprsión de la función es
Y la exprsión de la función es
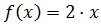 ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
Tipos de variables
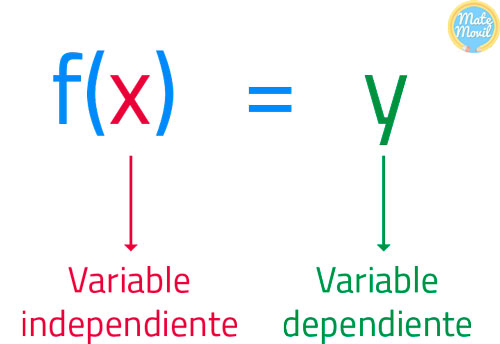
Variables dependientes. Son aquellas variables que como su nombre lo indica, dependen del valor que toma las otras variables Por ejemplo: «f(x) = x», «y o f(x)» es la variable dependiente ya que esta sujeta a los valores que se le subministre a «x».
Variable independiente. Es aquella variable que no depende de ninguna otra variable, en el ejemplo anterior la «x» es la variable independiente ya que la y es la que depende de los valores de «x».
Variable constante. Es aquella que no esta en función de ninguna variable y siempre tiene el mismo valor ejemplo: “y=2”, la constante gravitacional, entre otras.

Función de una variable
Cuando el valor de una variable “Y”
(función) depende de una sola variable “X”, tenemos una función de una
sola variable independiente.
Función de varias variables
Cuando el valor de una variable “Y”
depende de los valores de 2 ó más variables independientes.
Funciones Algebraicas
Son aquellas funciones cuyo valor puede
ser obtenido mediante un número finito de operaciones algebraicas (suma,
resta, multiplicación, división, elevación de potencias y la extracción de
raíces).Las funciones algebraicas se clasifican en:
Función racional
Es aquella cuyas variables no contienen
exponentes fraccionales ni se encuentran bajo signo de radical y se
expresa como el cociente de 2 funciones polinomiales.
Función irracional
Es aquella en la cual alguna de las
variables tienen exponentes fraccionarios o se encuentran bajo signo
radical.
Función entera
Es aquella que no tiene ninguna variable en el
denominador y no está afectada por exponentes negativos.
Función Polinomial
Son aquellas funciones que tienen la forma
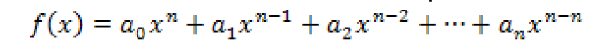 Donde n es un número entero positivo y
Donde n es un número entero positivo y
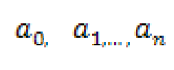 son números reales diferentes de cero
son números reales diferentes de cero
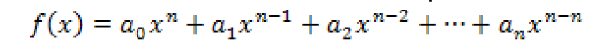 Donde n es un número entero positivo y
Donde n es un número entero positivo y
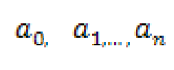 son números reales diferentes de cero
son números reales diferentes de ceroFunciones trascendentes
Se consideran como funciones
trascendentes a las exponenciales, logarítmicas, trigonométricas y
trigonométricas inversas
Funciones explicitas e implícitas
Sí están indicadas las
operaciones que hay que realizar con la variable o variables independientes
para obtener la función, se llama explícita. En caso contrario es función
implícita. Una función explícita se puede escribir en forma implícita y hay
funciones implícitas que pueden expresarse en función explícita.