Transformações do gráfico de uma função

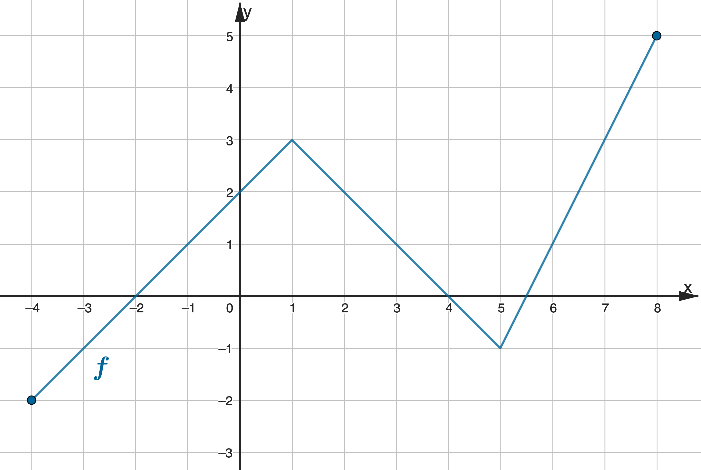
a) Indique o domínio e o contradomínio da função .

b) O gráfico de obtém-se a partir do gráfico de através de uma translação associada ao vetor de coordenadas:

c) Indique o domínio e o contradomínio da função se .

d) Indique o domínio e o contradomínio da função se .

a) O gráfico de obtém-se a partir do gráfico de através de uma translação associada ao vetor de coordenadas:

b) Indique o domínio e o contradomínio da função se .

c) Indique o domínio e o contradomínio da função se .

a) Indique o valor de tal que

b) A função , definida por transforma o ponto de coordenadas do gráfico da função no ponto de coordenadas:

a) Indique o domínio e o contradomínio da função se .

b) O valor de tal que é:

"O gráfico da função é a imagem do gráfico de por uma reflexão de eixo ."

b) O gráfico da função é a imagem do gráfico de por uma reflexão cujo eixo de simetria é o eixo: