Ponte a prueba: ¿qué sabes del volumen de cuerpos de revolución?
¿Qué entendemos por volumen?
Es una magnitud métrica de tipo escalar definida como la extensión en tres dimensiones de una región del espacio. Es una magnitud derivada de la longitud, ya que se halla multiplicando la longitud, el ancho y la altura.
Cuerpos geométricas o figuras geométricas (solidos) que delimitan volúmenes. ¿Sabrías el nombre de los tres cuerpos que aparecen? Piénsalo y comprueba tu respuesta en el test final.
¿Qué entendemos por sólido?
En el área de geometría, sólido indica a una figura u objeto que consta de 3 dimensiones: ancho, largo y profundidad, por ende, ocupa un lugar en el espacio y posee volumen, por ejemplo: la pirámide y el cono.
¿Sabrías describir las características vistas en clase de cada cuerpo? Piénsalo son muy intuitivas, verdad?
¿Sabrías describir las características vistas en clase de cada cuerpo? Piénsalo son muy intuitivas, verdad?
¿Qué entendemos por solido de revolucion?
Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que es contenida en su mismo plano. En principio, cualquier cuerpo con simetría axial o geométrica, es un sólido de revolució.
Recuerda lo visto en clase:
1. Tiene superficies curvas.
2. Tiene infinitos planos de simetría que contienen al eje.
3. No tiene aristas y por lo tanto, sus superficies no son polígonos.
4. Son generados por una figura plana que gira (Figura generatriz) sobre un lado recto que hace de eje de simetría.
5. Si la figura que lo genera (Figura generatriz) tiene un segmento perpendicular al eje, genera una cara circular.
6. Si la figura que lo genera (Figura generatriz) tiene un segmento diagonal al eje, genera una zona cónica.
7. Si la figura que lo genera (Figura generatriz) tiene un segmento paralelo al eje, genera una zona cilíndrica.
8. Si la figura que lo genera (Figura generatriz) tiene media circunferencia, genera una zona esférica o semiesférica, de acuerdo con la posición de la semicircunferencia.
9. Una figura genera un sólido diferente si cambia el eje de rotación.
Fíjate en las imágenes:
¿Sabrías nombrar y señalar los elementos necesarios para calcular de cada una su área y volumen?
Piénsalo, los necesitarás para responder el test final correctamente.
¿Sabrías nombrar y señalar los elementos necesarios para calcular de cada una su área y volumen?
Piénsalo, los necesitarás para responder el test final correctamente.
¿Qué entendemos por cono de revolución?
Es el sólido que se genera mediante la rotación completa de una región triángular alrededor de uno de sus catetos.
¿Sabrías escribir cuál es su fórmula del área y volumen? ¿ Y la relación que guarda el área con el volumen?
Jeje...leo tu mente pero reservarte para el test final.
¿Sabrías escribir cuál es su fórmula del área y volumen? ¿ Y la relación que guarda el área con el volumen?
Jeje...leo tu mente pero reservarte para el test final.
¿Qué entendemos por cilindro de revolución?
Es el sólido que se genera mediante una rotación de 360 grados de una región rectangular alrededor de uno de sus lados.
¿Sabrías escribir cual es su fórmula del área y volumen? Recuerda que tiene dos bases! Jeje....ya lo estarás destripando mentalmente en área lateral y áreas bases, cierto??
¿Sabrías escribir cual es su fórmula del área y volumen? Recuerda que tiene dos bases! Jeje....ya lo estarás destripando mentalmente en área lateral y áreas bases, cierto??
Fijate ahora en la siguiente construcción y observa como variando los valores del radio y la altura se generan distintos cilindros.
Te animo a ver este vídeo para aclarar las posibles dudas que aún te queden sobre cuerpos de revolucion!!
Cilindro: fórmula y ejemplo.
El volumen de un cilindro es el área de la base por la altura.
Consideremos un cilindro con radio de 4 centímetros y altura de 10 centímetros.
Para hallar el volumen de nuestro cilindro utilizamos la fórmula:
Sustituyendo valores tenemos:
Cono: fórmula y ejemplo.
El volumen de un cono es un tercio del área de la base por la altura.
Considerar un cono con radio de la base de 2 centímetros y una altura de 5 centímetros.
Para hallar el volumen de este cono utilizamos la fórmula:
Sustituyendo valores se tiene que:
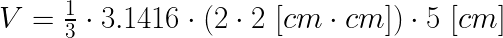
Para hallar el volumen de este cono utilizamos la fórmula:
Sustituyendo valores se tiene que:
Utiliza la hoja de geogebra para dibujar el solido que se forma al revolucionar el rectangulo por el lado de 8 cm
Empezamos a ponerte a prueba, ready?
Identifica la formula del volumen del cilindro
Calcula el área y el volumen de un cilindro recto cuya base mide 5.3 cm de radio y su altura es el triple del radio de la base.
Calcular el volumen de un cilindro de base 9 cm de diámetro y 7cm de altura
Que solido de revolución se forma al girar un rectángulo?
Identifica la formula del volumen del cono
Calcula el volumen de un cono de altura 4 cm y radio de la base 3 cm
Ahora vamos a complicar un poco la resolución. Necesitas una pista??
Aplicación del teorema de Pitagoras para conocer elementos desconocidos....
Calcula el volumen de un cono cuya generatriz mide 13 cm y el radio de la base 5cm
Para terminar vamos a darle a todo lo anterior un sentido práctico.
La altura de un embudo de hojalata, excluyendo el tubo de salida, mide 26 cm, y el diámetro, 30 cm. Si el metro cuadrado de hojalata pesa 3.25 kg, ¿ cuánto pesará el embudo?