Wahrscheinlichkeiten modellieren - Arbeitsauftrag Teil 1
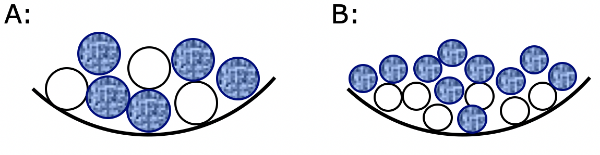
Aufgabe 1
Bei einer weißen Kugel gibt es einen Gewinn, die blauen Kugeln sind Nieten. Aus welchem Topf würden Sie eine Kugel ziehen, um zu gewinnen?
Aufgabe 2
Begründen Sie in ganzen Sätzen Ihre Antwort von Aufgabe 1.
*** Information ***
| | Als Wahrscheinlichkeit dafür, blind eine blaue Kugel aus Topf A zu ziehen, nimmt man nun den relativen Anteil der blauen Kugeln: P(blaue Kugel) = 5/8= 0,625 |
| Bsp. 1 | keine blaue Kugel im Topf | relativer Anteil blaue Kugeln = 0/8 = 0 | P(blaue Kugel) = 0 |
| Bsp. 2 | nur blaue Kugeln im Topf | relativer Anteil blaue Kugeln = 8/8 = 1 | P(blaue Kugel) = 1 |
| Bsp. 3 | vier blaue Kugeln im Topf | relativer Anteil blaue Kugeln = 4/8 = 0,5 | P(blaue Kugel) = 0,5 |
| | Sind die relativen Anteile und damit die Wahrscheinlichkeiten für alle Ergebnisse eines Zufallsexperiments gleich groß, so spricht man von einem Laplace-Experiment. |
Aufgabe 3
Es wird folgendes Zufallsexperiment gemacht: Aus einem Topf mit blauen und weißen Kugeln wird eine Kugel blind gezogen und die Farbe notiert. Welches der drei Beispiele von oben ist ein Laplace-Experiment?
Aufgabe 4
Auf einem Volksfest steht an einer Losbude ein Plakat mit der Aufschrift „Jedes 3. Los gewinnt!“. a) Der Betreiber der Losbude hat 900 Lose. Wie viele Lose müssen ein Gewinn sein, damit seine Werbung stimmt?
b) Alle Lose sind noch da. Das erste Los wird blind gezogen: Wie groß ist die Wahrscheinlichkeit, dass dieses Los eine Niete ist?
c) Ist das Ziehen des ersten Loses ein Laplace-Experiment?
Aufgabe 5
Aufgabe 6
Handelt es sich bei dem Würfel aus Aufgabe 3 um einen Laplace-Würfel?
Aufgabe 7
Gegeben ist ein Laplace-Würfel. Geben Sie die Wahrscheinlichkeit für folgende Ereignisse an und begründen Sie diese. a) Es wird die Zahl 6 gewürfelt.
b) Es wird eine 1, 2 oder 3 gewürfelt.
c) Es wird eine gerade Zahl gewürfelt.
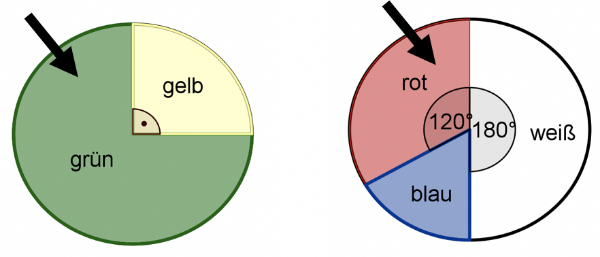
Aufgabe 8
Es wird ein Glücksrad gedreht. Ergänzen Sie zu den gegebenen Wahrscheinlichkeiten die passende Farbe. P(__________) = 1/6 P(__________) = 1/4 P(__________) = 1/3 P(__________) = 1/2
Aufgabe 9
Formulieren Sie ein passendes Ereignis zu folgenden Wahrscheinlichkeiten: P(A) = 3/4 P(B) = 2/3