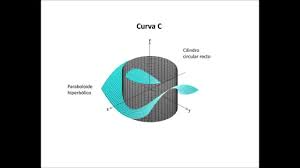
curvas en el espacio
curva en el espacio
Toda curva en el espacio R
n
se puede considerar como la imagen de una funci´on
vectorial
r : [a, b] → R
n
, r(t) = (x1(t), . . . , xn(t)),
que recibe el nombre de parametrizaci´on de la curva. Los puntos r(a) y r(b) son los
extremos inicial y final de la curva. En el caso de que r(a) = r(b), diremos que la
curva es cerrada.
Decimos que dos funciones ϕ : [a, b] → R
n y ψ : [α, β] → R
n
son equivalentes si existe
una funci´on λ : [a, b] → [α, β] biyectiva y continua tal que ψ ◦ λ = ϕ. La funci´on λ
recibe el nombre de cambio de par´ametro.
Dos funciones equivalentes representan parametrizaciones distintas de la misma curva
y la funci´on λ representa un cambio en la rapidez del movimiento.
- Si λ es creciente, se dice que las parametrizaciones ϕ y ψ conservan la orientaci´on
de la curva.
- Si λ es decreciente, las parametrizaciones ϕ y ψ invierten la orientaci´on de la curva.
Por ejemplo, las funciones
f1(t) = (cost,sen t), t ∈ [0, 2π],
f2(t) = (cost, − sen t), t ∈ [0, 2π],
f3(t) = (cos 2t,sen 2t), t ∈ [0, π],
representación grafica de una curva en el espacio