Definition des Funktionsbegriffs
Definition
Eine Funktion ist eine Zuordnung, die jedem Element einer Menge genau ein (!) Element einer anderen Menge zuordnet.
Man nennt die erste Menge Definitionsmenge D und die zweite Menge Wertemenge W.
Ein Beispiel einer Zuordnungsvorschrift einer Funktion:
In Worten: Die Funktion f ordnet jeder Zahl x ihre dritte Potenz x³ zu.
x³ nennt man auch den Funktionsterm, und die Funktionsgleichung. In der Mittelstufe schreibt man y anstelle von f(x), das heißt lautet bis zur 10. Klasse die Funktionsgleichung.
ist der sogenannte Funktionswert an der Stelle x.
Zum Beispiel ist der Funktionswert an der Stelle 2, nämlich 8.
Trägt man alle Punkte, die die sogenannte Punktprobe bestehen, das heißt deren y-Koordinaten die Funktionswerte an den jeweiligen Stelle (x-Koordinate) sind, in ein Koordinatensystem ein, so erhält man den Funktionsgraphen der Funktion. Manchmal sagt man auch Schaubild dazu.
Learning App (Überprüfung mit Button rechts unten)
Nichtfunktionale Zuordnung
Es gibt neben den Funktionen auch Zuordnungen, die keine Funktionen sind.
Zum Beispiel ist eine Zuordnung, die einer bestimmten Zahl zwei Zahlen zuordnet, keine Funktion.
Ein Anwendungsbeispiel:
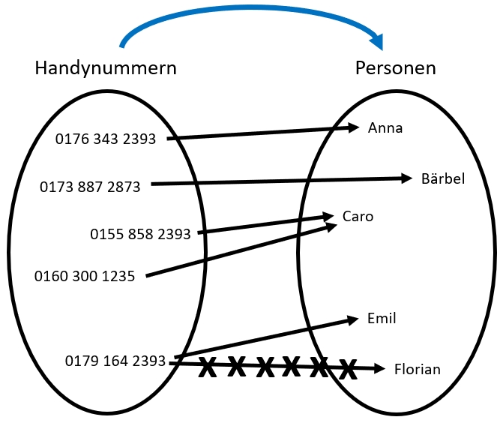
Es gibt eine Zuordnung, die jeder Telefonnummer eine Person zuordnet; das wäre eine Funktion, da zu jeder Telefonnummer genau eine Person gehört.
Umgekehrt kann ein und diesselbe Person jedoch mehrere Telefonnummern haben, z.B. da sie mehrere Handyverträge abgeschlossen hat. Die Zuordnung, die einer Person eine Telefonnummer zuordnet, ist also keine Funktion.
Umgangssprachlich könnte man sagen:
Eine Funktion ist eine dumme Maschine. Für einen Input muss sie exakt wissen, welchen Output sie ausgibt. Müsste die Maschine bei einem Input selbst entscheiden, welchen der mehreren Outputs sie jetzt gerade ausgibt, wäre sie keine Funktion.
Learning App
Punkte auf Graphen
Benutzen Sie den Schieberegler im folgenden Applet. Welche der Punkte liegen auf einem Graphen, der zu einer Funktion gehört?