Odvození souřadnic pólové ortografické projekce
- Autor:
- jirinaduspivova
Mějme zadaný bod A zeměpisnými souřadnicemi (φ, λ). Naším úkolem je zjistit, jaké kartézské souřadnice bude mít průmět A' bodu A v pólové ortografické projekci.
Z konstrukce situace v Mongeově promítání vyplývá, že poloměry rovnoběžkových kružnic se nezkreslují.
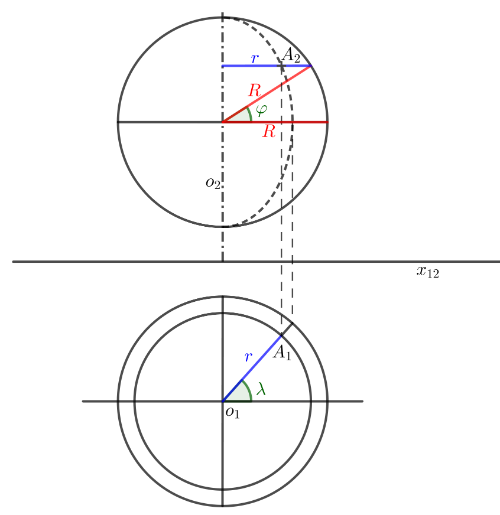
Vidíme, že půdorys je také pólovým ortografickým průmětem. Z vlastností goniometrických funkcí víme, že pro určení kartézských souřadnic prvního průmětu bodu A potřebujeme znát délku r. Pak můžeme vyjádřit průmět A' bodu A následovně
A' = [ xA, yA] xA = r cos λ yA = r sin λ
S určením délky r nám pomůže naopak nárys v Mongeově promítání. Odtud můžeme pomocí znalostí goniometrických funkcí určit, žer = R cos φ.
Po dosazení již známe kartézské souřadnice průmětu A' bodu AA' = [ R cos φ cos λ, R cos φ sin λ].