Moment of Inertia of a Rectangle

Fundamentally, the moment of inertia of a given area about a given axis tells you...

If the height h of the rectangle is doubled while the base b stays the same, how will the moment of inertia about its centroidal x’ axis change?

If the base b of the rectangle is tripled while the height h stays the same, how will the moment of inertia about its centroidal x’ axis change?

If the height h of the rectangle is doubled while the base b stays the same, how will the moment of inertia about its centroidal y’ axis change?

If the rectangle is translated one unit to the right with no change in b or h, how will the moment of inertia about its centroidal x’ axis change?

For a rectangle with b = 6 and h = 4 mm, which is the correct expression for the moment of inertia about the centroidal x’ axis?

For a rectangle with b = 6 and h = 4 mm, which is the correct expression for the moment of inertia about the centroidal y’ axis?

For a square with b = 4 and h = 4 mm, which is the correct expression for the moment of inertia about the centroidal x’ axis?

Which rectangle will have a greater moment of inertia about its centroidal x’ axis? Rectangle A: b = 3, h = 4 Rectangle B: b = 9, h = 2

Which rectangle will have a greater moment of inertia about its centroidal y’ axis? Rectangle A: b = 3, h = 4 Rectangle B: b = 9, h = 2

The moment of inertia of a given cross-sectional area about any axis other than its own centroidal axis, depends on which of the following terms?

Why does I_y increase when the square is translated to the right?

If a square is translated 2 units in the +x direction and 4 units in the +y direction with no change in its cross-sectional area, will this have a greater effect on I_x or I_y?

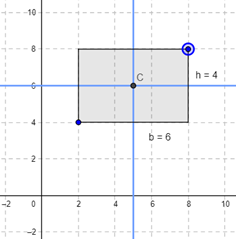
For the above rectangle, what is the correct expression for the moment of inertia of the area about the y-axis?

For the above rectangle, what is the correct expression for the moment of inertia of the area about the -axis?