La parábola (gráfica y ecuación)
LA PARÁBOLA
Definición:La parábola, es el lugar geométrico de todos los puntos de un plano, cuya distancia a un punto fijo llamado foco (F) es igual a la distancia a una recta fija llamada directriz (d). 1. Elementos de la parábola:
- Vértice (V): Punto de la curva que se interseca con el eje de simetría. El vértice es el punto medio entre el foco y la recta directriz.
- Foco (F): Punto ubicado sobre el eje de simetría, tal que su distancia a un punto cualquiera de la parábola es igual a la distancia entre ese punto y la directriz.
- Eje de simetría o eje focal: Recta perpendicular a la directriz, contiene al foco y al vértice.
- Directriz (d): Recta perpendicular al eje de simetría, su distancia a un punto cualquiera de la parábola a ella es igual a la distancia entre ese punto y el foco
- Lado recto (LR): Es la cuerda que pasa por el foco y es perpendicular al eje de simetría. La longitud del lado recto es 4 veces la distancia del vértice al foco. Esta distancia es el valor absoluto del parámetro p de la parábola. (LR = |4p|).
- Parámetro (p): Distancia del vértice al foco.
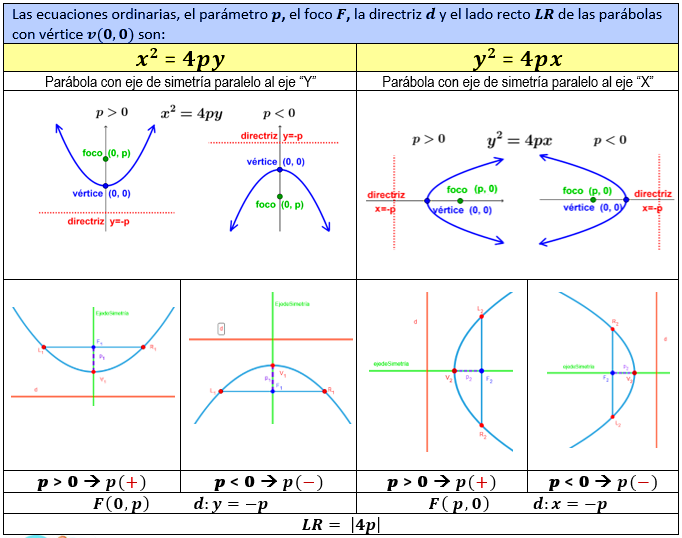
1.1. Ecuación de la parábola con vértice en el origen
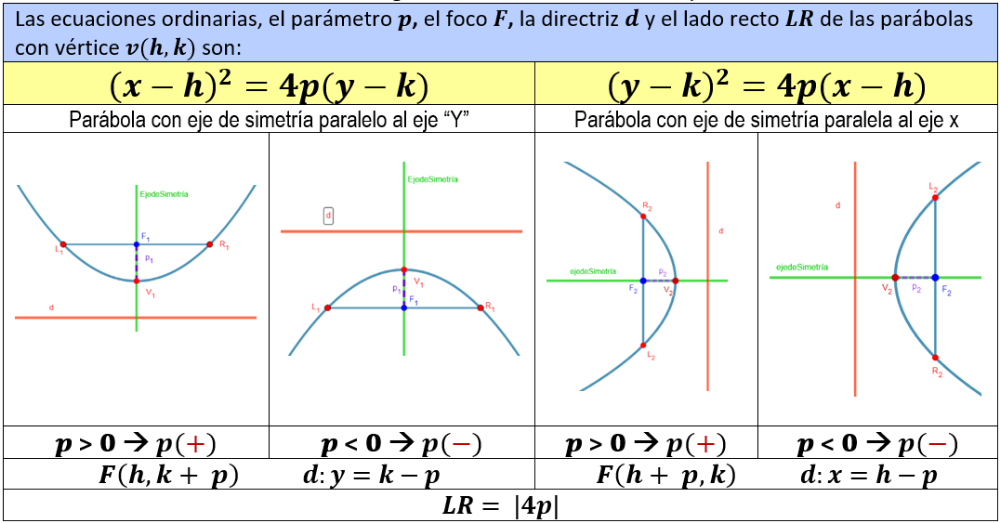
1.2. Ecuación de la parábola con vértice (h, k) fuera del origen