BASE BASE
Questão 1
Questão 2
Questão 2
Questão 3
Questão 4
Questão 5
Questão 6
Questão 7A
Em um quadrilátero ABCD qualquer, côncavo ou convexo, os pontos médios adjacentes de todos os seus lados podem ser ligados por segmentos de reta, formando um novo quadrilátero MNPQ. O quadrilátero MNPQ é necessariamente um paralelogramo? Sim / Não. Por quê? Justifique.
Questão 7B
Qual(is) propriedade(s) geométrica(s) do quadrilátero ABCD é(são) necessária(s) e suficiente(s) para que o quadrilátero MNPQ seja: Caso 1 - um losango; Caso 2 - um retângulo; Caso 3 - um quadrado.
Questão 8
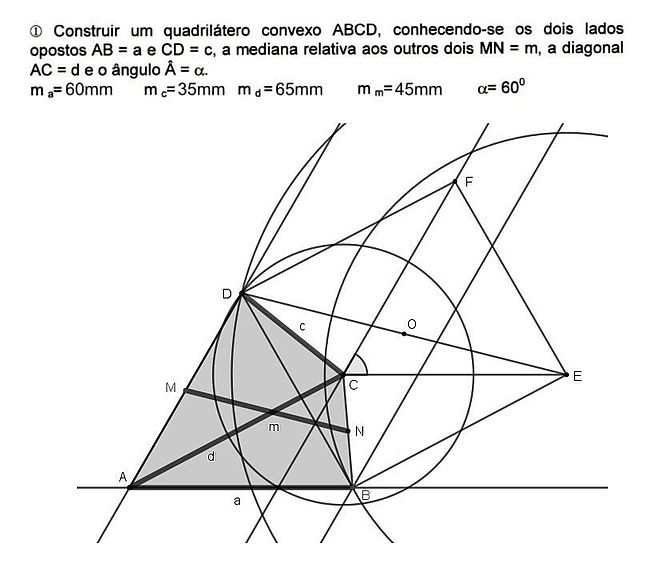
Dado o enunciado abaixo e a sua resolução completa, explique como o problema foi resolvido, do início ao fim, na ordem de construção. Considere que o primeiro segmento traçado foi o CE. Para cada ponto novo encontrado, informe os lugares geométricos usados para determiná-lo como elemento do conjunto de interseção.