Hipérbolas centradas en el origen.
Hipérbola horizontal.
En este caso tendremos una hipérbola con centro C=(0,0) y focos en el eje x, tal que
F1=(-c,0) y F2=(c,0).
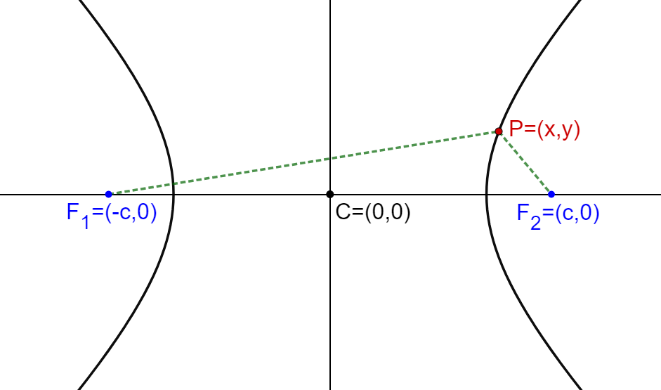
Siguiendo de la definición como lugar geométrico, tendríamos que un punto P pertenece a la hipérbola si se cumple que:
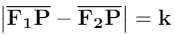
Donde k es una constante mayor que 1.
Utilizando la ecuación de distancia entre dos puntos, se traduce en:
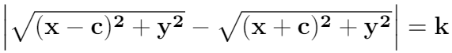
Para simplificar esta expresión tomemos en cuenta la siguiente figura:
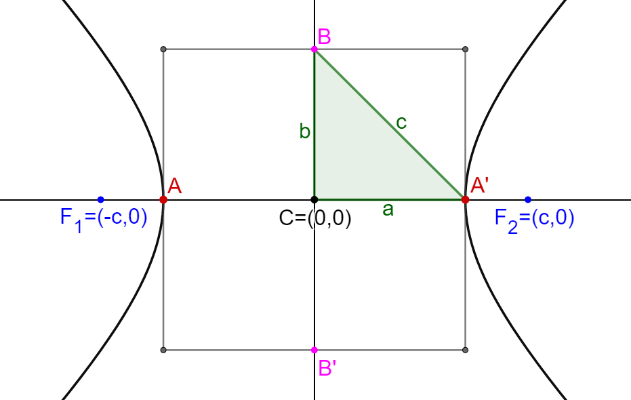
En el triángulo rectángulo ΔABC, el cateto a es el semieje transverso, el otro cateto es el semieje conjugado b. Se puede demostrar que la hipotenusa c es igual a la semidistancia focal.
Sustituimos k=2a en la ecuación anterior, y simplificando se llega a la ecuación:
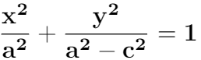
Aplicando el teorema de Pitágoras en ΔABC de la figura anterior se obtiene .
Sustituyendo:
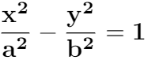
Hipérbola vertical.
En este caso tendremos una hipérbola con centro C=(0,0) y focos en el eje x, tal que
F1=(0,-c) y F2=(0,c).
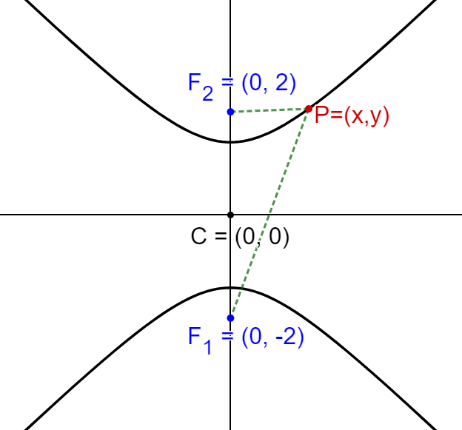
Denominando como 2a a la diferencia de las distancia de un punto P de la hipérbola a los focos, y realizando un análisis similar al del caso de la hipérbola horizontal, (o simplemente intercambiando los papeles de las variables), se llega a la siguiente ecuación:
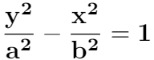
Actividad
Encontrar cuál es la ecuación de la siguiente hipérbola: