Trigonometrische Funktionen in der Praxis
Natur und Technik
In Natur und Technik spielen Schwingungen wie Schallwellen udn Lichtwellen sowie sich regelmäßig wiederholende Vorgänge wie Ebbe und Flut eine wichtige Rolle.
Mithilfe von Sinusfunktionen oder Cosinusfunktionen können solche Vorgänge beschrieben werden.
Dazu wird die Funktionsgleichung an die Gegebenheiten angepasst. Durch entsprechende Transformationen erhält man eine allgemeine Sinusfunktion bzw. Cosinusfunktion. Sinus- oder Cosinusfunktionen nennt man auch trigonometrische Funktionen.
Beispiel Ebbe und Flut im Hafen
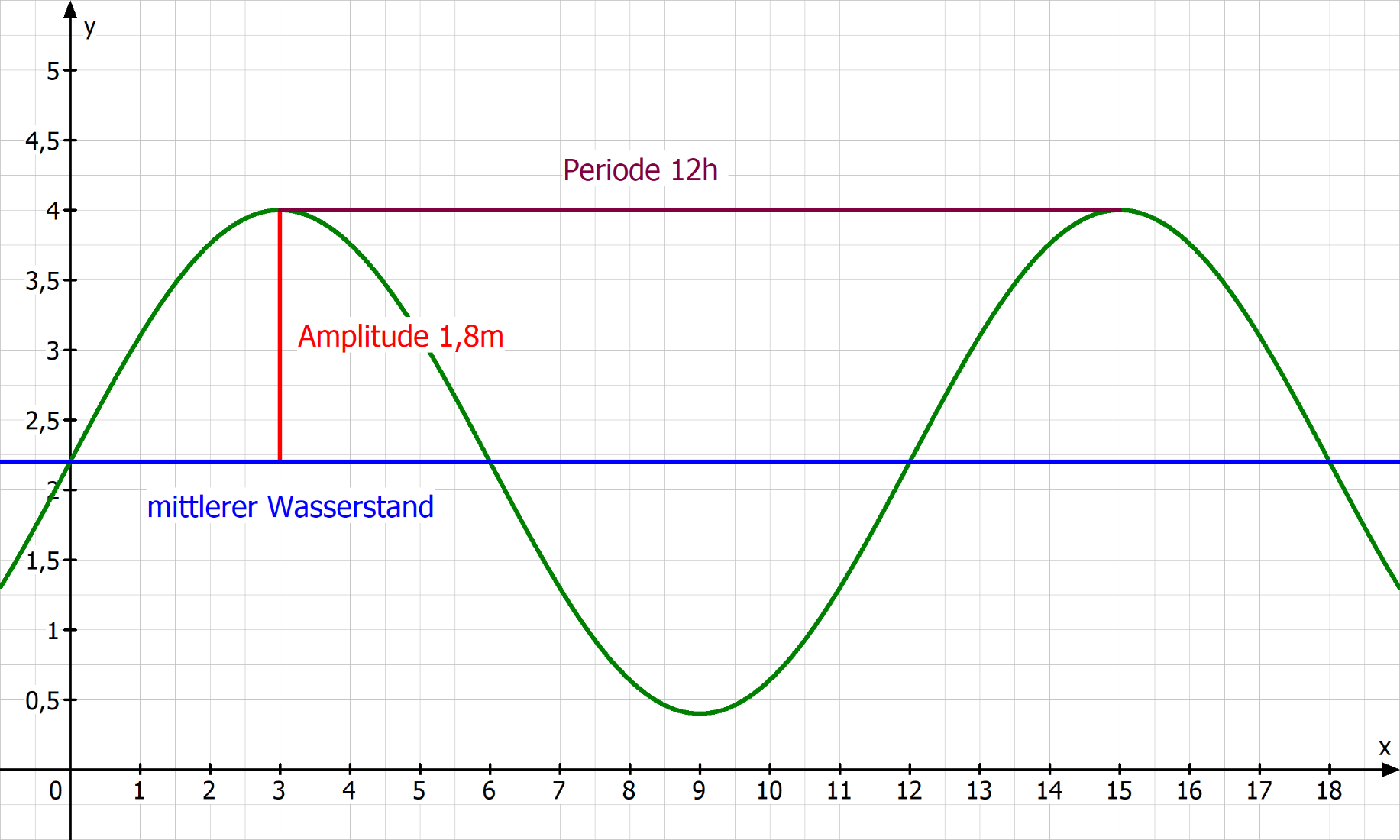
Das Schaubild unterhalb zeigt den Wasserstand im Hafen an einem Sommertag.
Er schwankt zwischen dem Höchststand von 4m um 3:00 Uhr (t=3) und dem Tiefstand von 0,40 um 9:00 Uhr (t=9).
Die maximale Abweichung vom mittleren Wasserstand (2,20m um 0:00 Uhr) nennt man Amplitude .
Sie beträgt hier 1,80m. Um 15:00 Uhr wird erneut der Höchststand von 4,00m erreicht. Der Pegelstand wiederholt sich periodisch alle 12 Stunden.
Um eine passende Funktionsgleichung zu bestimmen, betrachtet man die Grundfunktion f mit f(x) = sin (x). Das Schaubild von f hat die Amplitude 1 und die Periode 2. Nun wird das Schaubild der Sinusfunktion entsprechend gestreckt bzw. verschoben.
Nach allen Transformationen erhalten wir folgendes Schaubild:
Ebbe/Flut