Otras operaciones con matrices
Trasposición de matrices
Se llama matriz traspuesta de una matriz A de dimensión m x n a la matriz que se obtiene al cambiar en A las filas por columnas, o las columnas por filas. Se representa por At y su dimensión es n x m. Si la matriz es cuadrada, su traspuesta tiene el mismo orden.
Las principales propiedades de la trasposición de matrices son:
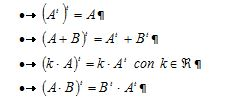
Matrices simétricas y antisimétricas
La trasposición de matrices permite definir dos nuevos tipos de matrices:
- Se llama matriz simétrica a toda matriz cuadrada que coincide con su traspuesta A = At. Se puede ver que toda matriz simétrica tiene iguales los elementos simétricos respecto de la diagonal principal.
- Se llama matriz antisimétrica o hemisimétrica a toda matriz cuadrada que coincide con la opuesta de su traspuesta A =-At. Los elementos de una matriz antisimétrica son iguales y opuestos respecto de la diagonal principal y cuyos elementos son, a su vez, nulos.

Ejercicios de matrices
Utiliza el siguiente applet de Geogebra para realizar los ejercicios indicados en el archivo anterior:
