解方程组
任务
求鞍点为 (1, 1) 和 (2, 2) 的三次多项式函数.
指导
| 1. |  | 在指令栏, 定义函数 f(x):= a x^3 + b x^2 + c x + d. |
| 2. | p | 根据任务, 函数在 x=1 时的值是 1. 输入 p: f(1) = 1; , 然后按 Enter 键. 窍门: 冒号 ":" 是定义方程式, 而分号 “;” 是阻止输出. |
| 3. | q | 我们也知道函数在 x=2 时的值是 2. 在指令栏输入 q: f(2) = 2; |
| 4. | r | 因为 (1, 1) 是一个鞍点, 所以在 x=1 处的一阶导数等于 0. 输入 r: f'(1) = 0;
窍门: f 的导数可写为 f'. |
| 5. | s | 我们也知道, 在 x=1 处的二阶导数等于 0. 输入 s: f''(1) = 0; |
| 6. | 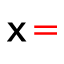 | 用指针选择第二到第五行, 然后应用精确解工具. |
| | | 窍门:
|
| 7. | Substitute | 在指令栏输入 Substitute($1, $6), 然后按 Enter 键.
注意: 您这是用刚计算出来的解集 ($6) 替换公式 f ($1) 中未定义的变量. |
| 8. |  | 激活行号 7 中禁用的可见性按钮, 在  绘图区绘制函数. |