Fußballfeld mit Bande ... oder nicht? | CamCarpets
Das hast Du bestimmt auch schon einmal erlebt: Du schaust ein Fußballspiel, rechts und links vom Tor die üblichen Werbebanden und dann: Ein Spieler läuft ohne zu bremsen und auf die Werbeaufsteller zu und ... steht plötzlich direkt darauf.
Quelle: https://3dsportsigns.com/liga-santander-2020-camcarpets-3dcarpets
Diese sogenannten Cam Carpets sind zweidimensionale Matten, die nur aus der richtigen Kameraperspektive heraus dreidimensional wirken. In dieser Aktivität geht es darum, selber Cam Carpets mit GeoGebra zu erzeugen.
Cam Carpets "von Hand" konstruieren
Um einen Cam Carpet "von Hand" zu erstellen, konstruiert man die zum Kamerastrahl parallelen Geraden durch die Eckpunkte der Figur, die als Cam Carpet dargestellt werden soll. Der Cam Carpet entsteht, wenn man die Schnittpunkte dieser Geraden mit der xy-Achse (quasi dem "Boden") verbindet. Der mathematische Fachbegriff für eine solche Abbildung ist "Parallelprojektion".
Probiere das für den folgenden Buchsten "L" aus. Verändere auch die Position und Blickrichtung der Kamera und beobachte, wie sich der Cam-Carpet aus verschiedenen Perspektiven verändert.
Unter anderem die folgenden Befehle helfen Dir bei der Konstruktion:
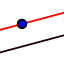zu einem Vektor oder einer anderen Gerade parellele Gerade durch einen Punkt erstellen
Schnittpunkt von zwei Objekten (z.B. Gerade und Ebene)
Objekte ein/ausblenden
Lösungsvorschlag
Hier findest Du eine fertige Konstruktion zur oberen Aufgabe.
Cam Carpets schnell mit Matrizen ausrechnen
Das oben beschriebene Konstruktionsverfahren ist für kompliziertere Figuren (wie dem nachfolgenden MATHE-Schriftzug) sehr aufwendig, schnell unübersichtlich und rechenintensiv. Eine effizientere Lösung nutzt eine Matrix zur Beschreibung der Parallelprojektion.
Hier kommen Tipps, wie Du in GeoGebra einfach die Matrix (abhänging vom Kameravektor) aufstellen kannst.
- Die Spalten einer Darstellungsmatrix entsprechen den Bildern der drei Einheitsvektoren (1,0,0), (0,1,0) und (0,0,1)
- In GeoGebra schreibt man eine Matrix als Liste von Listen, dabei stellen die inneren Listen die Zeilen dar. Es gilt also:
{{a,b,c},{d,e,f},{g,h,i}}= - Für einen Punkt
P=(a,d,g)kann man mitx(P),y(P)undz(P)auf die einzelnen Komponenten zugreifen. Es gilt also z.B.x(P) = a. - Mit dem Befehl
MatrixAnwenden(<Matrix>, <Objekt> )kann man dann eine Matrix auf ein Objekt (z.B. ein Vieleck) anwenden.