La flor de Venus
Esta actividad pertenece al libro de GeoGebra La Tierra y el Sol.
Cada 8 años, Venus da casi exactamente 13 vueltas alrededor del Sol. En ese tiempo, Venus adelanta 5 veces a la Tierra, generando una cáustica que recuerda a 5 cardioides entrelazadas (sería una cardioide si el año terrestre durase el doble que el venusiano).
En la construcción, PULSA EL BOTÓN REPRODUCIR (esquina inferior izquierda, apenas se ve).
 | Más precisamente, la fracción de los períodos orbitales entre ambos planetas (365,256/224,701) está muy próxima a ser 13/8 (1+5/8). Por tanto, el ciclo relativo se repite cada 8/5=1,6 años, que equivale a 576º (una vuelta y 216º) de vueltas terrestres, lo que provoca la aparición de ese patrón pentagonal conocido como pentagrama o flor de Venus. |
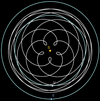 | Como las trayectorias de Venus y la Tierra son casi circunferencias, obtenemos el mismo diagrama sustituyendo el segmento Tierra-Venus por su punto medio PM. También obtenemos el mismo diagrama como un epiciclo de Venus visto desde la Tierra, sin más que ajustar la escala de las distancias a la mitad. Esto se debe a que si sumamos la mitad del vector Sol-Tierra con la mitad del vector Sol-Venus, obtenemos precisamente el vector Sol-PM. |
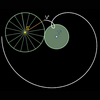 | Suponiendo que las trayectorias de Venus y la Tierra fueran circunferencias perfectas y la relación 13/8 fuera exacta, la flor de Venus sería una epitrocoide perfecta, es decir, podría ser generada por una gigantesca rueda que rodase (sin deslizamiento) sobre un círculo centrado en la Tierra con radio 5/13 de la distancia de la Tierra al Sol. |
Notas:
3. La construcción ha sido realizada con los datos reales de la Tierra y Venus, pero se puede simplificar mucho usando circunferencias en vez de elipses, sin que se aprecie diferencia alguna dada su pequeña excentricidad. También se puede usar directamente la relación 13/8.
 |  | 1. La flor de Venus se puede materializar fácilmente mediante hilos tensados (hiloramas). Es muy conocido por los aficionados a la astrología y otras pseudociencias, de modo que se puede encontrar su diseño en todo tipo de objetos, como en joyería. |

| 2. La imagen del diagrama que aparece en la construcción proviene de la entrada "epiciclo" en Wikipedia - Movimiento aparente (J. Ferguson 1710-1776 basado en un diagrama similar de G. Cassini 1625-1712). |
Autor de la actividad y construcción GeoGebra: Rafael Losada.