The Bernoulli Number

A large number of common functions have power-series expansions whose coefficients can be expressed in terms of a set of numbers first identified by Jacques Bernoulli. These so-called Bernoulli numbers also appear in other mathematical contexts; they are found in formulas for the Riemann zeta functions of even integer argument, and they enter in the Euler-Maclaurin summation formula (which relates the integral of a function to a sum over discrete values of the same function). They are also of interest from a pedagogical viewpoint; their definition and properties illustrate the concept and use of generating functions and recurrence formulas.
The Bernoulli numbers  are a sequence of signed rational numbers that can be defined by the exponential generating function
are a sequence of signed rational numbers that can be defined by the exponential generating function
These numbers arise in the series expansions of trigonometric functions, and are extremely important in number theory and analysis. There are actually two definitions for the Bernoulli numbers. To distinguish them, the Bernoulli numbers as defined in modern usage (National Institute of Standards and Technology convention) are written 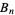 , while the Bernoulli numbers encountered in older literature are written
, while the Bernoulli numbers encountered in older literature are written 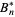 (Gradshteyn and Ryzhik 2000). In each case, the Bernoulli numbers are a special case of the Bernoulli polynomials
(Gradshteyn and Ryzhik 2000). In each case, the Bernoulli numbers are a special case of the Bernoulli polynomials 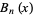 or
or 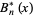 with
with 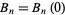 and
and 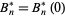 .
The Bernoulli number and polynomial should not be confused with the Bell numbers and Bell polynomial, which are also commonly denoted
.
The Bernoulli number and polynomial should not be confused with the Bell numbers and Bell polynomial, which are also commonly denoted 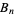 and
and 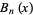 , respectively. Bernoulli numbers defined by the modern definition are denoted
, respectively. Bernoulli numbers defined by the modern definition are denoted 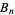 and sometimes called "even-index" Bernoulli numbers. These are the Bernoulli numbers returned, by example, by the Wolfram Language function Bernoulli B[n].The Bernoulli number
and sometimes called "even-index" Bernoulli numbers. These are the Bernoulli numbers returned, by example, by the Wolfram Language function Bernoulli B[n].The Bernoulli number 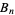 can be defined by the contour integral
can be defined by the contour integral
where the contour encloses the origin, has a radius less than 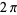 (to avoid the poles at
(to avoid the poles at 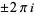 ), and is traversed in a counterclockwise direction (Arfken 1985, p. 413).The first few Bernoulli numbers
), and is traversed in a counterclockwise direction (Arfken 1985, p. 413).The first few Bernoulli numbers 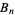 are:
are: