Definição e alguns resultados

Iniciamos o estudo sistemático da geometria dos quadriláteros. Dentre os vários tipos particulares de quadriláteros que vamos considerar aqui, os principais são, certamente, os paralelogramos, qualificados na definição a seguir: Definição: Um quadrilátero convexo é um paralelogramo se possuir lados opostos paralelos.

Observação: uma vez que estamos trabalhando com polígonos é importante ressaltar que sempre consideramos o seu interior, mesmo que muitas vezes este não seja ressaltado durante as proposições e demonstrações realizadas neste material. ABCD paralelogramo AB || CD e AD || BC . No que segue, vamos enunciar várias maneiras equivalentes de definir paralelogramos. O leitor deve guardar tais resultados como propriedades notáveis dessa classe de quadriláteros, a serem usadas oportunamente. Proposição_1: Um quadrilátero convexo é um paralelogramo se, e só se, seus ângulos opostos forem iguais.

A partir das proposições acima, sabemos que um paralelogramo é um quadrilátero de lados opostos paralelos, assim como que a medida destes lados opostos são iguais. Pode ocorrer, entretanto, que saibamos somente que dois lados opostos de um quadrilátero são paralelos, podendo ou não possuir medidas iguais. Neste caso, diremos que tal quadrilátero é um trapézio.

Paralelogramo Trapézio

Em todo trapézio, os dois lados sabidamente paralelos são suas bases, sendo o maior deles a base maior e o menor deles denominado base menor. Os outros dois lados (sobre os quais nada sabemos, mas que podem também ser paralelos, caso o trapézio seja, em particular, um paralelogramo) são os lados não paralelos do trapézio.

Antes de prosseguir, precisamos de mais algumas convenções acerca de trapézios, quais sejam: o segmento que une os pontos médios dos lados não paralelos de um trapézio é a base média do mesmo, ao passo que o segmento que une os pontos médios das diagonais de um trapézio é sua mediana de Euler.

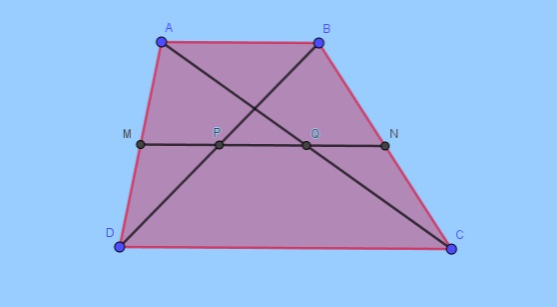
A proposição a seguir nos ensina como calcular os comprimentos de tais segmentos em termos dos comprimentos das bases do trapézio.

Proposição_4: Seja ABCD um trapézio de bases AB e CD e lados não paralelos AD e BC. Sejam, ainda, M e N os pontos médios dos lados não paralelos AD e BC, respectivamente, e P e Q os pontos médios das diagonais AC e BD, também respectivamente. Então: (a) M, N, P e Q são colineares e MN AB, CD. (b) MN = . (AB + CD) e PQ = . |AB - CD| .

Link para o "resultado *" descrito durante a demonstração acima, que se refere a propriedade das bases médias de um triângulo: < > A fim de completar nosso estudo dos tipos particulares mais elementares de quadriláteros, vamos estudar, agora, retângulos e losangos. Um quadrilátero (convexo, como sempre) é um retângulo se todos os seus ângulos internos forem iguais. Mas, como sabemos, a soma dos ângulos internos de um quadrilátero é sempre igual a 360º, segue que um quadrilátero é um retângulo se, e só se, todos os seus ângulos internos forem iguais a 90º. Um quadrilátero é um losango se todos os seus lados forem iguais. _____________________________ Como os lados opostos de um retângulo são sempre paralelos (uma vez que são ambos perpendiculares a um qualquer dos outros dois lados), todo retângulo é um paralelogramo.



Retângulo Paralelogramo Por outro lado, a proposição_2 deste material, nos garante que todo losango também é um paralelogramo. Losango Paralelogramo Observe que a recíproca de ambos os casos não é verdadeira!

Há um último tipo de quadrilátero que desejamos estudar, o quadrado. Um quadrilátero é um quadrado quando for simultaneamente um retângulo e um losango. Assim, quadrados são quadriláteros de ângulos e lados iguais; ademais, suas diagonais são também iguais e perpendiculares, se intersectam no meio e formam ângulos de 45º com os lados do quadrilátero. (Prove essa última afirmação!)