Nullstellen und Krümmung einer linearen Funktion - Didaktischer Kommentar
Kurzbeschreibung
Diese Aktivität erfordert die Kenntnis vieler Eigenschaften zu funktionalen Abhängigkeiten von den Schülerinnen und Schülern. Deswegen sollte diese Aufgabe wohl überlegt eingesetzt werden, wenn tatsächlich alle vorkommenden Inhalte zuvor schon genügend behandelt wurden, da ansonsten die Lernenden schnell die Motivation zur Bearbeitung dieser Aufgabe verlieren können. Wichtig sind hier die Begrifflichkeiten Krümmungsverhalten, Steigung, Nullstellen, Funktionswert und Argument einer linearen Funktion.
Kompetenzen
Die Schülerinnen und Schüler können ...
- die allgemeine Form der Funktionsgleichung einer linearen Funktion angeben und interpretieren.
- das Verhalten der Krümmung vom Graphen einer linearen Funktion deuten.
- die Steigung einer linearen Funktion anhand zweier gegebener Punkte des Graphens berechnen.
- das Verhalten bezüglich der Nullstellen einer linearen Funktion erklären.
- angeben, dass sich der Funktionswert immer um den konstanten Wert ändert, wenn das Argument um 1 erhöht wird.
Kopiervorlage für Schülerinnen und Schüler
Lösungen
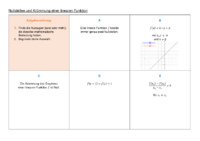
- Bei Aussage B handelt es sich um die Zielaussage in Form der allgemeinen Funktionsgleichung einer linearen Funktion samt dynamischem Schaubild mit Schiebereglern.
- Aussage C hat dieselbe mathematische Bedeutung wie die Zielaussage B, da es sich hier lediglich um eine andere Darstellungs- bzw. Repräsentationsform handelt. Es wird eine Eigenschaft über das Krümmungsverhalten des Graphen einer linearen Funktion thematisiert.
- Aussage E teilt ebenfalls dieselbe mathematische Bedeutung wie die Zielaussage B, es handelt sich hier um die äquivalente Darstellungs- bzw. Repräsentationsform, da dieselbe Art von Zeichensystem verwendet wird. Diese Aussage lässt die Steigung einer linearen Funktion anhand zweier gegebener Punkte berechnen.
- Aussage D hat nicht dieselbe mathematische Bedeutung wie die Zielaussage B, da diese Aussage für eine lineare Funktion nicht wahrheitsgemäß ist, denn: der Funktionswert ändert sich immer um den konstanten Wert , wenn das Argument um 1 erhöht wird. Diese Aussage erscheint in derselben Darstellungs- bzw. Repräsentationsform wie B.
- Aussage A hat nicht dieselbe mathematische Bedeutung wie die Zielaussage B, da diese Aussage nicht stimmt für eine lineare Funktion. Eine lineare Funktion hat immer genau eine Nullstelle. Diese Aussage verwendet nicht dieselbe Darstellungs- bzw. Repräsentationsform wie die Zielaussage, da hier eine andere Art von Zeichensystem verwendet wird.