Exerciseurs : comment ça marche ?
Un premier exemple
Prenons ce modèle simple d'exerciseur :
https://www.geogebra.org/m/v8tdrysm
dont une copie est ci-dessous. Nous allons expliquer comment il est construit pour que vous puissiez le modifier ou en fabriquer selon le même principe.
Pour voir à l'intérieur :
Construction
Ci-dessus, la fenêtre propriétés à droite est ouverte ce qui rend les boutons inactifs mais permet de voir dans les différents menus : couleur, style, script et dans avancé l'affichage conditionnel pour chaque objet sélectionné.
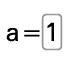dans le menu curseur 
qui joue le rôle de "input(reponse)". On pouvait aussi taper dans la barre de saisie :
- Aléatoire :
AléaEntreBornes(-10, 10)
Ils représentent ici les deux nombres à additionner.
Ces valeurs sont réactualisées par le bouton Recommencer dont le script commence par :
ActualiserConstruction()- Question :
- Valeur cible :
- Champ réponse :
reponse indéterminée au début par reponse=?
Ensuite un créé un champ de saisie avec 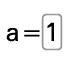dans le menu curseur qui joue le rôle de "input(reponse)". On pouvait aussi taper dans la barre de saisie : ChampTexte(reponse)- Tester si la réponse est correcte.
correct= reponse==cible est évalué en true si la réponse est correcte, false sinon.
Modifier ce fichier
Si vous voulez modifier légèrement cette appliquette sans tout chercher à comprendre, voici quelques pistes.
- Modifier l'aléatoire :
AléaEntreBornes(1, 30). Si vous ne souhaitez additionner que des multiples de 10 : AléaEntreBornes(1, 10)*10, ou des nombres décimaux avec un chiffre après la virgule : AléaEntreBornes(1, 1000)/10. Pour éviter d'avoir la valeur 0 tout en ayant des nombres positifs ou négatifs, on peut utiliser :
AléaEntreBornes(1, 9)*(2*AléaEntreBornes(0, 1)-1)
Le deuxième facteur (2*AléaEntreBornes(0, 1)-1) valant -1 ou 1 joue le rôle du signe et peut aussi être utile par ailleurs.
- Tester l'égalité d'objets autres que des nombres.
reponse et cible peuvent par exemple contenir des droites. Mais on peut souvent se ramener à tester l'égalité de nombres, par exemple en testant si un déterminant ou un produit scalaire est nul pour savoir si des droites sont parallèles ou perpendiculaires.
Voir par exemple cet exercice du livret pour un test de produit scalaire.
Pour tester l'égalité entre deux expressions algébriques, il est préférable de les comparer sous forme simplifiée avec la fonction Simplifier( ). Par exemple dans cet exercice du livret, pour tester si l'expression de la dérivée est correcte, le booléen correct est défini par :
correct=Simplifier(Dérivée(foncalea))≟Simplifier(reponse)
Couleurs pour une rétroaction visible en mode Classroom.
La suite rentre dans des détails de codage qui peuvent être ignorés en première lecture si vous voulez simplement modifier cette appliquette pour faire un exerciseur.
- Rétroaction avec fond coloré
SoitValeur(valide,true)
SoitValeur(coul,Si(correct,2,1))
La deuxième ligne signifie que Si la réponse est correcte, alors la variable coul prend la valeur 2 et sinon elle prend la valeur 1.
Cette variable coul sert juste à changer la couleur du fond de l'écran, vous pouvez dans l'appliquette ci-dessus la faire varier de 0 à 3 :
coul=0 : pas de couleur (fond noir)
coul=1 : fond orange (réponse incorrecte)
coul=2 : fond vert (réponse correcte)
coul=3 : fond rouge (appel à l'aide)
- Les couleurs
fond dont la couleur dépend de la variable coul. Si vous regardez dans l'onglet Avancé pour le polygone fond, vous verrez que les codes RGB dépendent de coul et de la liste Couleur={1, 0.8, 0.2, 0.4, 0.8, 0, 1, 0.2, 0.4}. Cette liste Couleur contient 9 nombres. Les trois premiers sont 1, 0.8, 0.2 ce qui correspond à la couleur orange de code RGB=(1,0.8,0.2) il faut multiplier par 255 pour avoir l'équivalent sur la palette. De même les trois suivants sont pour vert et les 3 derniers pour rouge. L'opacité est réglée à 0.25 (soit 25%) sauf si coul=0 auquel cas le fond est transparent (opacité=0).