Retos. Estadística y probabilidad
Reto 1.
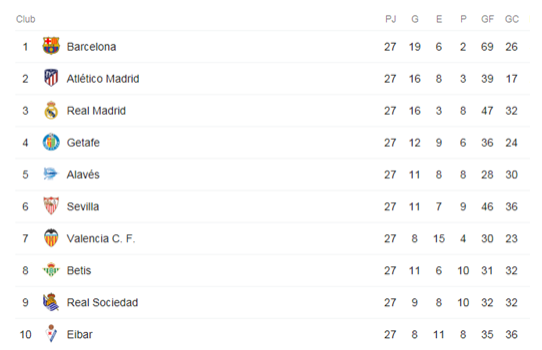
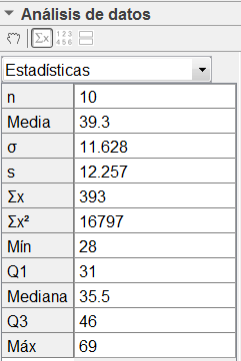
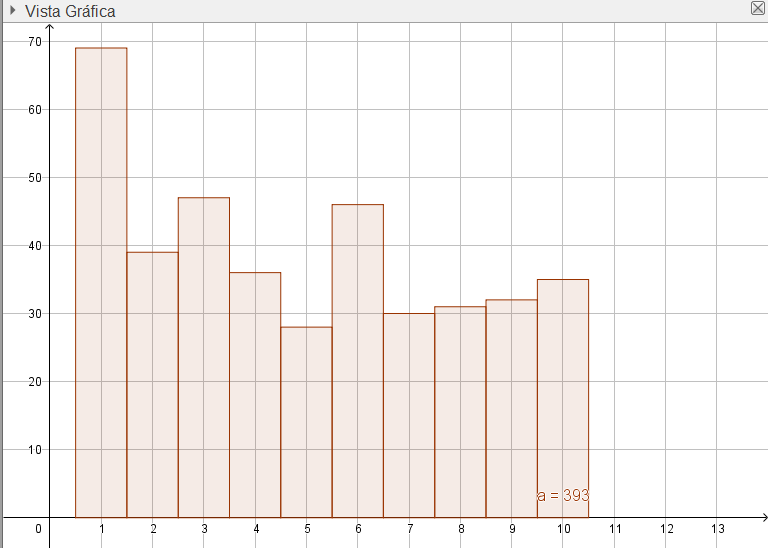
Las dos últimas columnas de la siguiente tabla recogen los goles a favor (GF) y los goles en contra (GC) de
los diez primeros equipos de futbol de la liga española. Representa en un diagrama los goles a favor o los goles en contra, calculando la media y desviación típica de estos datos.
Reto 2.
Construye un diagrama de sectores para los datos siguientes:
| Dato | Valor |
| A | 10 |
| B | 15 |
| C | 24 |
| D | 32 |
| E | 44 |
Reto 3.
Si disponemos de ocho puntos en el plano, de los que no hay más de dos puntos alineados.
- ¿Cuántas rectas se pueden trazar utilizando los puntos anteriores?
- ¿Cuántos triángulos se pueden construir a partir de los puntos anteriores?
- ¿Y cuántos polígonos de cuatro lados se pueden dibujar con los puntos anteriores?
- Intenta generalizar para obtener cuántos polígonos de n lados se pueden dibujar con los puntos anteriores.
- ¿Cuál es la razón por la que se pide que no haya más de dos puntos alineados?
Las respuestas a las cuestiones anteriores son las siguientes:
1. Como la recta AB es la misma que la recta BA, las posibles rectas serán las combinaciones de ocho elementos tomados de dos en dos, por lo que el cálculo se obtiene a partir del comando:
nCr(8,2)=28
2. Al igual que antes, el triángulo ABC será el mismo que el triángulo BCA. Por tanto, serán nCr(8,3)=56
3. Lo mismo para los polígonos de cuatro lados. Será nCr(8,4)=70
4. Para n lados, con 3<=n<=8, se podrán dibujar un total de nCr(8,n)=8!/n!(8-n)!
5. Si hay más de dos puntos alineados, por ejemplo ABC, estos puntos no formarán un triángulo y lo mismo ocurrirá para cualquier lado de un polígono de más lados.