L7.2 - Inscribed Angles
Learning Intentions and Success Criteria
- Calculate measures of central and inscribed angles.
- Use the relationship between central and inscribed angles to prove (using words and other representations) a theorem about intersecting chords.
- Use the relationship between central and inscribed angles to calculate angle measures and prove geometric theorems.
- Know that an inscribed angle is half the measure of the central angle that defines the same arc.
2.1: Notice and Wonder: A New Angle
What do you notice? What do you wonder?
2.2: A Central Relationship
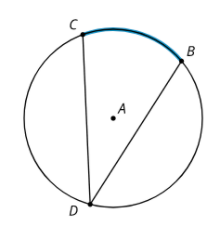
In Google classroom under classwork open Geo.7.2 Inscribed Angles to use the applet in 2.2: A Central Relationship. Use the applet to answer the questions. Do not show the angle measures until you are told to. 1. Name the central angle in this figure. 2. Name the inscribed angle in this figure.
3. Move point B around the circle. As you move this point, what happens to the measure of angle QBC? Show the angle measures to confirm.
4. Move points C, Q and B to new positions. Record the measure of angles QAC and QBC. Repeat this several times.
5. Make a conjecture about the relationship between an inscribed angle and the central angle that defines the same arc.
2.3: Similarity Returns
The image shows a circle with chords CD, CB, ED and EB. The highlighted blue arc from point C to point E measures 100 degrees. The highlighted orange arc from point D to point B measures 140 degrees. Prove that triangles CFD and EFB are similar.

Learning Intentions and Success Criteria
- Calculate measures of central and inscribed angles.
- Use the relationship between central and inscribed angles to prove (using words and other representations) a theorem about intersecting chords.
- Use the relationship between central and inscribed angles to calculate angle measures and prove geometric theorems.
- Know that an inscribed angle is half the measure of the central angle that defines the same arc.
Cool-down: Inscribed Angle Measures
The measure of the pink arc from B to A not passing through C is 30 degrees. 1. What is the measure of angle BOA? 2. What is the measure of angle BDA? 3. What is the measure of angle BCA?