Relaciones de Conjuntos
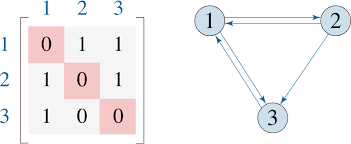
En matemáticas, una relación es un conjunto de pares ordenados que establece una conexión o asociación entre elementos de dos conjuntos. Supongamos que tenemos dos conjuntos, A y B. Una relación R entre A y B se representa como RAxB, donde AxB es el producto cartesiano de A y B, que consiste en todos los pares ordenados posibles (a, b) tales que aA y bB. Las relaciones pueden representarse mediante tablas, gráficos o descripciones explícitas de los elementos relacionados.
Propiedades de las Relaciones:
Existen varias propiedades que las relaciones pueden poseer:
1. Reflexiva: Una relación R en un conjunto A es reflexiva si cada elemento en A está relacionado consigo mismo. En otras palabras, (a, a)R para todo aA.
2. Simétrica: Una relación R en un conjunto A es simétrica si, para cada (a, b)R, también (b, a)R.
3. Transitiva: Una relación R en un conjunto A es transitiva si, para cualesquiera elementos a, b y c en A, si (a, b)R y (b, c)R, entonces (a, c)R.
Conjunto de Relaciones:
El conjunto que contiene todas las relaciones posibles entre dos conjuntos dados A y B se denota como P(AxB), donde P denota el conjunto potencia (conjunto de todos los subconjuntos) de AxB. En otras palabras, el conjunto de relaciones es la colección de todos los subconjuntos del producto cartesiano AxB.