1. Teoría del color
DE LUZ Y DE COLOR
Publicado en la sección Geometría dinámica y Matemáticas interactivas de Divulgamat
Junio 2010
Propiedad Color Dinámico en GeoGebra
La propiedad Color Dinámico que poseen los objetos creados con GeoGebra permite visualizar fácilmente lugares geométricos desconocidos, siempre que sepamos expresar la condición que deben cumplir los puntos del mismo.
Este modo de empleo del color dinámico es realmente potente. Simplemente "barriendo" la pantalla el lugar geométrico aparece, como por arte de magia, ante nuestros ojos.
Esta propiedad Color Dinámico asigna al objeto tres valores numéricos, cada uno de ellos variable entre 0 y 1, que corresponden a la intensidad de Red, Green y Blue (color RGB) presentes en su color-luz combinado.
En la siguiente tabla se puede apreciar (agrupados por complementarios) el resultado de la elección de algunos colores básicos.
Cuando el valor numérico "c" no esté entre 0 y 1, GeoGebra sigue la siguiente norma:
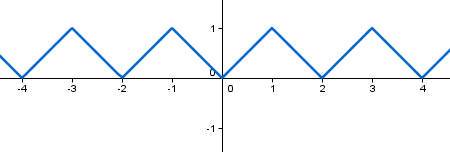El motivo de este comportamiento es evitar cambios bruscos de color entre dos valores numéricos próximos. Obsérvese el periodo 2.
Así, si construimos un punto A y una paralela al eje Y que contenga a A y le asignamos a esta recta el color dinámico que denotaremos como RGB = [0, x(A), 0]:
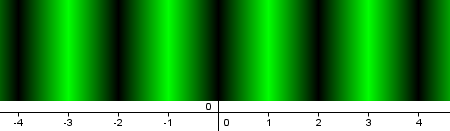
entonces, al activar el rastro de la recta y moverla obtendremos una distribución de color que sigue el patrón que muestra la siguiente imagen.
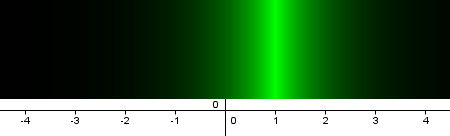
Si se quiere evitar la periodicidad, podemos optar por sustituir la expresión x(A) por la expresión e^(-abs(x(A)-1)).
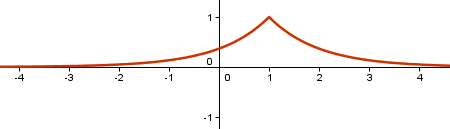
La gráfica de la función y = e^(-abs(x-1)) es la siguiente:
por lo que al realizar la sustitución obtenemos una distribución de color del siguiente tipo:
Cuando el valor numérico "c" no esté entre 0 y 1, GeoGebra sigue la siguiente norma:
- Si el valor numérico no está entre 0 y 2, toma su resto módulo 2.
- Si el valor numérico "c" obtenido está entre 1 y 2, toma "2 - c".
c(x) = 1 - abs(1 - x + 2 floor(x/2))
cuya gráfica es:
El motivo de este comportamiento es evitar cambios bruscos de color entre dos valores numéricos próximos. Obsérvese el periodo 2.
Así, si construimos un punto A y una paralela al eje Y que contenga a A y le asignamos a esta recta el color dinámico que denotaremos como RGB = [0, x(A), 0]:
entonces, al activar el rastro de la recta y moverla obtendremos una distribución de color que sigue el patrón que muestra la siguiente imagen.
Si se quiere evitar la periodicidad, podemos optar por sustituir la expresión x(A) por la expresión e^(-abs(x(A)-1)).
La gráfica de la función y = e^(-abs(x-1)) es la siguiente:
por lo que al realizar la sustitución obtenemos una distribución de color del siguiente tipo: