Aplicações
Teorema 1: O volume de um prisma qualquer é dado pelo produto da sua altura pela sua
base.
Demonstração:
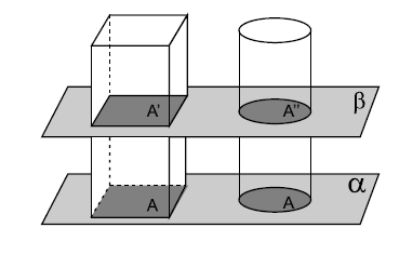
Considere um prisma de altura h e área da base A e o plano no qual a base está contida.
Considere também um paralelepípedo reto retângulo de altura h cuja base inferior, também contida no plano , tenha área A. Além disso, considere um plano , paralelo a , cuja distância com relação a seja h0.
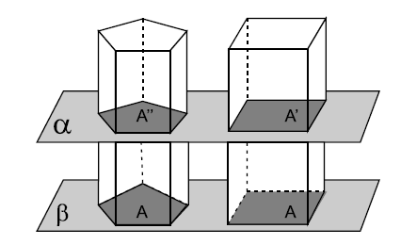
Assim, obtemos duas secções transversais de áreas A′ e A′′, no paralelepípedo e no prisma, respectivamente. Como o paralelepípedo, em particular, é um prisma e toda secção feita por um plano paralelo à base de um prisma determina uma figura congruente à base, obtemos que A′ = A = A′′. Como os dois prismas possuem a mesma altura h e as secções feitas paralelas à base determinam figuras equivalentes, e, portanto, possuem a mesma área, então, pelo Princípio de Cavalieri, podemos concluir que os volumes destes sólidos são iguais.
Teorema 2: O volume de um cilindro circular é dado pelo produto da área de sua base pela altura do cilindro.
Demonstração:
A demonstração deste teorema é análoga à demonstração do teorema 1.
Dado um cilindro circular com área da base A e altura h, construa um paralelepípedo de base A e altura h. Como A′ = A = A′′ e a área do cilindro é igual a A · h, segue, pelo Princípio de Cavalieri, que os dois sólidos possuem o mesmo volume e, portanto, o volume V do cilindro é tal que V = A · h.