Contenuti
Etude des Coniques
Les explications permettant d'élaborer les figures de ce recueil sont accessibles dans le document suivant au format PDF :
https://mathmj.fr/geogebra/coniques/coniques.pdf
Sommario
Introduction
- Figure I.1 Cylindre
- Figure I.2 : cône
- Figure I.3 sphère inscrite dans un cône
- Figure I.4 : angle entre plan et droite
- Figure I.5 I.6 et I.7 : Les 3 sections Coniques non dégénérées
- Figure IV.6 : théorèmes de Poncelet
- Figure IV.7 : lieu du mileu d'une corde de direction fixée
- Figure IV.8 : parabole tangente au 3 côtés d'un triangle
Ellipse
- Figure II.1 ellipse vu comme section plane d'un cylindre
- Figure II.2 : Section conique elliptique
- Figure II.3 : cône passant par tous les points d'une ellipse
- Figure II.4 : projection d'une ellipse selon un cercle
- Figure II.5 : construction de l'ellipse par foyers et cercle directeur
- Figure II.6 : points et cercles remarquables
- Figure II.7 : cordes conjuguées d'une ellipse
- Figure II.8 théorèmes d'Appolonius
- Figure II.9 : cercles de Chasles
- figure II.10 : Construction par bande de papier
- Figure II.11 : directrices d'une ellipse
- Figure II.12 : directrices et excentricité
- Figure II.13 : Equation en coordonnées polaires
- Figure II.14 : tangentes en les extrémités passant par un foyer
- Figure II.15 : théorème de Poncelet
- Figure II.16 : ellipse inscrite dans un triangle
- Figure II.17 : cercle orthoptique
Hyperbole
- Figure III.1 : section conique hyperbolique
- Figure III.2 : lieu du sommet d'un cône passant par une hyperbole
- Figure III.3 et III.4 : contruction par foyers et cercle directeur
- Figure III.5 : construction des tangentes
- Figure III.6 : points et cercles remarquables d'une hyperbole
- Figure III.7 : Hyperbole rapportée à ses asymptôtes
- Figure III.8 cordes et diamètres conjugués d'une hyperbole
- Figure III.9 : lieu du milieu des cordes parallèles entre elles
- Figure III.10 : Théorèmes de Poncelet (points de contact sur mea même branche)
- Figure III.11 : Théorèmes de Poncelet (Points de contacts sur des branches distinctes)
- Figures III.12 et III.13 : hyperbole tangente aux trois côtés d'un triangle.
- Figures III.14 et III.15 : lieu orthoptique d'une hyperbole.
- Figure III.16 : directrices d'un hyperbole
- Figures III.17 et III.18 : équation en coordonnées polaires
- Figures III.19 et III.20 : Tangentes et directrices (polaire du foyer)
Parabole
Synthèse + quelques coniques Célébres
- Figure V.1 : theoreme de pascal
- Figure V.2 : theoreme de pascal (bis)
- Figure V.3 : Construction à la règle, pointpar point d'une conique passant par 5 points fixés
- Figure V.4 : contruction à la règle d'une tangente en un point d'une conique
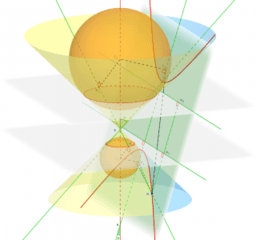
- Figure V.5 : théorème de Dandelin
- Figure V.6 : démonstration du théorème de Dandelin
- Figure V.7a : coordonnées du sommet d'un cône passant par une ellipse
- Figure V.7b : ellipse et son hyperbole focale
- Figure V.8a : sommet d'un cône passant par une hyperbole
- Figure V.8b ; hyperbole et son ellipse focale
- Figure V.9.a : Sommet d'un cône passant par une parabole
- Figure V.9b : paraboles focales l'une de l'autre
- Figure V.10 : définition de l'isogonalité
- Figure V.11 : conjugaison isogonale par rapport à un triangle
- Figure V.12 : Conjugaison isogonale dans un triangle
- Figure V.13 : conjugué isogonal d'un point sur le cercle circonscrit rejeté à l'infini
- Figure V.14 : la conjugaison isogonale d'une droite est une conique
- Figure V.15 : Conjugué isogonal d'un point sur cercle circonscrit
- Figure V.16 : Conjugués isogonaux à l'intérieur du triangle
- Figure V.17 : conjugué isogonal d'un point à l'intérieur du cercle circonscrit mais à l'extérieur du triangle.
- Figure V.18 : points isogonaux à l'extérieur du cercle circonscrit
- Figure V.19 : ellipse exinscrite dans un triangle
- Figure V.20 : ellipse inscrite dans un triangle avec 2 points de contacts imposés
- Figure V.21 : hyperbole exinscrite dan un triangle avec deux points de contacts imposés
- Figure V.22 : recherche d'une conique de centre O fixé passant par 3 points fixés.
- Figure V.23 parbole tangente aux trois côtés d'un triangle, avec un point de contact imposé
- Figure V.24 : construction d'une conique avec centre fixé, tangente aux 3 côtés d'un triangle
- Figure V.26 : parabole de Miquel d'un quadrilatère
- Figure V.25 : point de Miquel d'un quadrilatère complet
- Figure V.26 : parabole de Miquel d'un quadrilatère complet
- Figure V.27 : ellipse d'Euler
- Figure V.28 : Hyperbole d'Euler dans un triangle
- Figure V.29 : les 2 ellipses de Steiner d'un triangle
- Figure V.30 : projection orthogonale d'une ellipse selon un cercle
- Figure V.31 : Point K parcourant l'hyperbole de Kiepert
- Figure V.32 : hyperbole-Kiepert
Annexes