Função Quadrática
Definição:
Toda função do segundo grau apresenta algumas características. Ela deve ser dos conjuntos
dos números Reais para os Reais (R em R), essa função é expressa pela função
f(x)= ax2 + bx +c, sendo a, b, c números reais e a 0.
Exemplo:
f(x)=3x2+5x-5
f(x)=x2+3x-28
Propriedades Gráficas:
O gráfico da Função Polinomial do 2º Grau y = ax2+ bx + c
é uma parábola cujo eixo de simetria é uma reta vertical (x), paralela ao
eixo y ou até mesmo o próprio eixo y, passando pelo vértice da parábola.
Observe que o eixo de simetria intercepta o eixo x (eixo das
abcissas) num ponto equidistante das raízes, além de interceptar a parábola em
seu ponto de máximo ou em seu ponto de mínimo. A parábola terá ponto de máximo
ou de mínimo de acordo com a sua concavidade. Observe isso atentamente agora.
Concavidade da parábola:
Concavidade é a distância entre as duas pontas da parábola. A parábola pode ter a concavidade voltada para cima ou para
baixo. A parábola tem a concavidade voltada para cima quando a > 0
enquanto tem a concavidade voltada para baixo quando a < 0.
Observe:
a>0 a<0
Relação com o delta:
Os zeros da função quadrática y=ax2+bx+c, são as raizes da equação do segundo grau correspondentes ax2+bx+c=0, cujo a natureza depende do discriminante delta(Δ), os zeros da função y=ax2+bx+c são os valores onde a parábola pode cruzar ou não o eixo X, veja a seguir:
Para Δ>0:
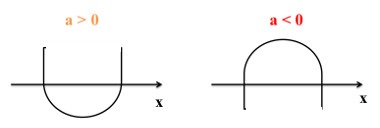Para Δ=0:
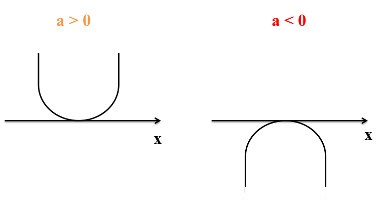Para Δ<0:
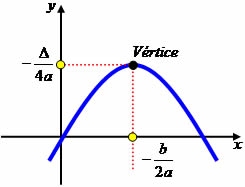
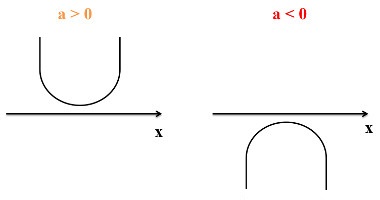Coordenadas do Vértice de uma Parábola.
O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas. O eixo horizontal é chamado de abcissa (x) e o vertical de ordenada (y). Os eixos são enumerados
compreendendo o conjunto dos números reais. O x do vértice é expresso pela formula x =−b/2a
Observe que o eixo de simetria intercepta o eixo x (eixo das
abcissas) num ponto equidistante das raízes, além de interceptar a parábola em
seu ponto de máximo ou em seu ponto de mínimo. A parábola terá ponto de máximo
ou de mínimo de acordo com a sua concavidade. Observe isso atentamente agora.
Concavidade da parábola:
Concavidade é a distância entre as duas pontas da parábola. A parábola pode ter a concavidade voltada para cima ou para
baixo. A parábola tem a concavidade voltada para cima quando a > 0
enquanto tem a concavidade voltada para baixo quando a < 0.
Observe:
a>0 a<0
Relação com o delta:
Os zeros da função quadrática y=ax2+bx+c, são as raizes da equação do segundo grau correspondentes ax2+bx+c=0, cujo a natureza depende do discriminante delta(Δ), os zeros da função y=ax2+bx+c são os valores onde a parábola pode cruzar ou não o eixo X, veja a seguir:
Para Δ>0:
Para Δ=0:
Para Δ<0:
Coordenadas do Vértice de uma Parábola.
O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas. O eixo horizontal é chamado de abcissa (x) e o vertical de ordenada (y). Os eixos são enumerados
compreendendo o conjunto dos números reais. O x do vértice é expresso pela formula x =−b/2a
Video explicação:
Qualquer duvida:
Objetivos
• Fazer uma explicação direta do conteúdo de funções
quadráticas.
• Auxiliar o estudo e a compreensão sobre função quadrática;
• Melhorar o entendimento de gráficos com parábolas.
• Resolver exercícios que envolvam equação do segundo
grau.
•Aplicar as formulas da função
quadrática em problemas do dia a dia
Justificativa
Esclarecer dúvidas e/ou ensinar outros alunos, tanto de ensino médio como de ensino fundamental, que viram ou não esse conteúdo e a como aplicar as formulas de delta, bhaskara, Xv e Yv e aplica-las em questões que envolvam gráficos com parábolas. Na matemática os gráficos de funções do segundo grau, são de eximia importância para a resolução de varias atividades. Isso ira melhorar o domínio da teoria sobre função quadrática dessa maneira ira desenvolver um raciocínio logico dos alunos.
Apostila matematica-FUNÇÃO QUADRÁTICA
Texto:
http://brasilescola.uol.com.br/matematica/funcao-segundo-grau.htm
http://educacao.globo.com/matematica/assunto/funcoes/funcao-de-2-grau.html
http://mundoeducacao.bol.uol.com.br/matematica/funcao-2-grau.htm
http://www.somatematica.com.br/emedio/funcao2/funcao2.php
https://www.tutorbrasil.com.br/aulas-de-matematica/funcoes-2-grau/vertice-e-imagem-funcao-2-grau/
Vídeos de referência:
https://www.youtube.com/watch?v=dRakRUoltfo
https://www.youtube.com/watch?v=1wNK4wuHx1Q
https:/www.youtube.com/watch?v=7t0PwH8QevQ&feature=youtu.be
1)Determine qual das seguintes equações tem as seguintes raízes: -0,4 ; 1.
2) O vértice da parábola y = 2x2 - 4x + 5 é o ponto:
3) A distância do vértice da parábola y= -x2 + 8x - 17 ao eixo das abcissa (x e y do vértice) é:
4)Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abcissa.
5) Um avião ao levantar voo, cria uma parábola, expressa pela fórmula 5x2-3x-2=0. Sabendo que a altura é representada pelo Y do vértice (Yv), e a distância percorrida pelo X do vértice (Xv), Determine que altura o avião atingiu e à que distância.