Función Sobreyectiva
1.6 Función Sobreyectiva
Introducción
Una función fes sobreyectiva (o suprayectiva) si todo elemento del conjunto final Y tiene al
menos un elemento del conjunto inicial X al que le corresponde.
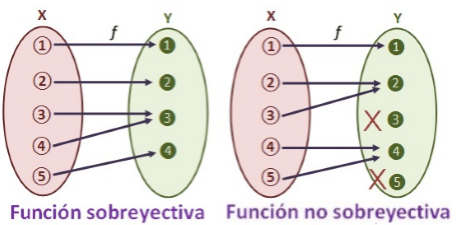
Es decir, una función es sobreyectiva si el recorrido de la función es el conjunto final Y.
En términos matemáticos, f es suprayectiva.
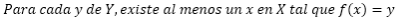
Supuesto de aplicación
Enseguida proporcionamos un ejercicio matemático y ejemplos de aplicaciones cotidianas.
Por ejemplo: Determinar si:
f(x)= 3x + 2 , es sobreyectiva:
- Hacemos f(x) = y
- Despejamos "x":
- En problemas de optimización en los planteamientos de problemas de estructura multiplicativa o del agente viajero, donde se tienen que ocupar todos los nodos que van del lado 1 al lado 2.
- En finanzas cuando a cada portafolio inversión le corresponde uno o más inversionistas.