Bruchungleichungen - Erklärung
Definition
Unter einer Bruchungleichung verstehen wir eine Ungleichung, die mindestens einen Bruchterm enthält. Ein Bruchterm ist ein Bruch, dessen Nenner eine Variable enthält.
Zu beachten ist:
- Bruchungleichungen lassen sich wie auch Ungleichungen durch Äquivalenzumformungen lösen.
- Zuvor muss man jedoch die Definitionsmenge des Bruchterms bestimmen (Nenner beachten!).
- Wie von Ungleichungen bekannt, muss bei einer Multiplikation oder Divison der Ungleichung mit einer negativen Zahl das Relationszeichen umgekehrt werden.
- Wird eine Bruchungleichung mit einer Variable multipliziert oder dividiert, muss eine Fallunterscheidung gemacht werden.
Bruchungleichung Beispiel 1
Versuche, das folgende Beispiel nachzuvollziehen. Im Anschluss ist eine Erklärung dazu gegeben.
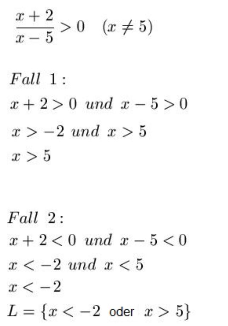
- Zunächst wird die Definitionsmenge bestimmt. So darf für x nicht 5 in die Ungleichung eingesetzt werden, da sonst eine Division durch Null erfolgen würde.
- Anschließend überlegen wir uns, die Bedingungen, für die ein Bruch größer als Null wird. Dies ist bei Fall 1, wenn Zähler und Nenner größer Null sind oder bei Fall 2, wenn Zähler und Nenner kleiner Null sind.
- Fall 1 wird durch bekannte Äquivalenzumformungen gelöst. schließt mit ein, daher ist die Lösungsmenge zu Fall 1.
- Fall 2 wird durch bekannte Äquivalenzumformungen gelöst. schließt mit ein, daher ist die Lösungsmenge zu Fall 2.
- Diese Bruchungleichung hat also zwei Lösungen, diese werden in der Lösungsmenge mit einem "oder" verbunden.
Bruchungleichungen Beispiel 2
Zunächst wird auch bei diesem Beispiel wieder die Definitionsmenge bestimmt.
Anschließend erfolgt die Fallunterscheidung dahin gehend, dass der Nenner einmal größer als Null und einmal kleiner als Null ist.
1. Fall: Der Nenner ist größer als Null. Berechne die Bedingung dafür. Anschließend können wir in der Ungleichung mit Äquivalenzumformungen die Lösungsmenge anschreiben.
2. Fall: Der Nenner ist kleiner als Null. Berechne die Bedingung dafür. Anschließend können wir in der Ungleichung mit Äquivalenzumformungen die Lösungsmenge anschreiben.
Die gesamte Lösungsmenge ist die Vereinigung der Lösung von Fall 1 und Fall 2.
Lasse dir anschließend im Grafikfenster die Lösungsmenge und Funktionen noch anzeigen.