Potenzfunktion mit rationalem Exponenten - Wurzelfunktion II
Vorbetrachtung
Bevor wir auf den neuen Typ von Potenzfunktionen eingehen, soll eine kleine Vorbetrachtung stehen.
Wann ist eine Funktion eine Funktion?
Im Folgenden entdeckst du einen weiteren Typen von Potenzfunktionen.
Aufgabe 1
a) Stelle bei den Schiebereglern m=4 und n=2 ein
b) Stelle bei den Schiebereglern m=9 und n=3 ein
Wie sehen die Funktionsgraphen aus?
zu Aufgabe 1
Wie du sicher festgestellt hast, gibt es spezielle Fälle, in denen der neue Typ der Potenzfunktionen wie alte Bekannte aussieht.
Schauen wir nun auf die anderen Fälle, in denen der Exponent keine ganze bzw. natürliche Zahl ist.
Aufgabe 2
a) Stelle die Schieberegler auf m=1 und n=2. Klicke nun auf "Umkehrfunktion anzeigen".
b) Stelle die Schieberegler auf m=1 und n=3. Klicke nun auf "Umkehrfunktion anzeigen".
Wie sehen die Umkehrfunktionen aus?
Aufgabe 3
Klicke auf "Spiegelgerade anzeigen" und überlege, warum sie so heißt.
Lies erst weiter, wenn du zu einer Vermutung gekommen bist.
Dir sollte aufgefallen sein, dass die Funktionen durch Spiegelung an der Winkelhalbierenden des 1. Quadranten auseinander hervorgehen.
zu Aufgabe 2 und 3
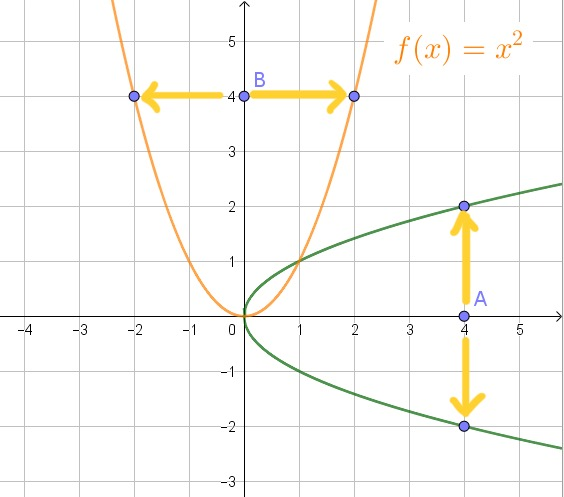
Warum ist die Umkehrfunktion nur eine "halbe Parabel" - d.h. nur für x-Werte eingezeichnet, die größer oder gleich der Null sind? Man könnte doch eine "ganze" Normalparabel () an der Spiegelgeraden spiegeln?
Die oben untersuchten Potenzfunktionen des Typs heißen Wurzelfunktionen. Wie das obere Applet verdeutlicht, sind Wurzelfunktionen nur für nichtnegative x-Werte definiert.
Die Umkehrfunktionen von Wurzelfunktionen ergeben "Teil-"Potenzfunktionen. Diese sind auf nichtnegative x-Werte beschränkt. Dementsprechend sind Wurzelfunktionen ebenso die Umkehrfunktionen auf ebendiese beschränkten Potenzfunktionen.
Aufgabe 4
Der einfache Fall ist dabei, wenn der Exponent des Radikanten "m" den Wert "1" annimmt.
Die daraus entstehende Potenzfunktion würde dann die n-te Wurzel von x abbilden.
Somit kann diese auch als Wurzelfunktion bezeichnet werden.
Bewege den Schieberegler, um die nachfolgenden Fragen zu beantworten:
Welchen Definitions- und Wertebereich haben Wurzelfunktionen?
Welches Monotonieverhalten haben Wurzelfunktionen?
Welche(n) Punkt(e) haben alle Wurzelfunktionen gemeinsam?
Aufgabe 5
Auch Wurzelfunktionen unterliegen einem Parametereinfluss.
Doch du kannst unbesorgt sein - du weißt bereits, wie dieser sein wird.
Im Folgenden hast du ein Applet, welches alle Parametereinflüsse zusammenfasst. Unter diesem findest du abschließende Kontrollfragen.
Parameter a
Der Parameter a beeinflusst:
Parameter d
Der Parameter d beeinflusst:
Parameter e
Der Parameter e beeinflusst:
Zusatz 1
Wenn du noch etwas knobeln willst, dann kannst du gerne die Umkehrfunktion herleiten.
Dafür tauscht du in der folgenden Gleichung x mit y und löst nach y auf:
Zur Kontrolle kannst du in das obige Applet schauen. Dort ist die Umkehrfunktion angegeben.
Zusatz 2
Wir haben gesagt, dass die Wurzelfunktionen nur für nichtnegative x-Werte definiert sind.
Jedoch kann man die dritte Wurzel aus "-8" ziehen. Diese ist "-2".
Die Gegenprobe - d.h., "-2" hoch "3" - zeigt, dass dies stimmt.
Überlege dir, warum es zu Problemen kommen könnte.
Die Lösung findest du auf folgender Seite:
https://www.studysmarter.de/schule/mathe/analysis/wurzelfunktion/