Nex21 (4,1) [2/3] - Diagram
I tried to calculate the strut lengths using Nsolve.
Unfortunately, Geogebra does not come up with a solution.
I therefore use Chris Kitrick's calculations.
New Nexorade/Rotegrity project : 19 jan 2019 18:58:43
Chris Kitrick,
I will explain the solution to the next simplest nexorage: nex21 (4,1) [Taff's 2v{1,1}].
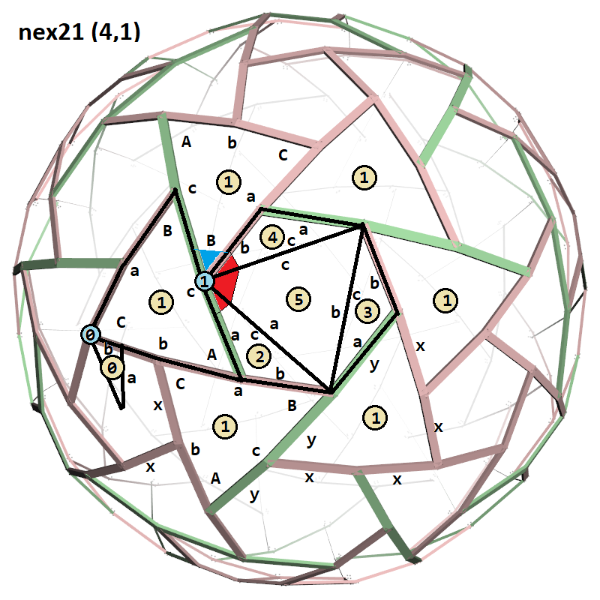
A diagram that illustrates the spherical triangle composition is attached.
Now there are six (6) unique spherical triangles to consider.
Due to symmetry triangle 0 is a right triangle at the pentagonal vertex
(same as the first case).
Triangle 1 is an isosceles spherical triangle with side a equal to side b.
There are two large blue dots indicating the two unique places
where the joining corners of spherical triangles must add up to 180 (π).
Keeping the 1/3 arc division you see there are only two arcs
one composed of (3x) and the other (3y).
Even though we now have two unknowns (x,y) there is really only one
unknown (x), since (y) has a direct relationship to (x).
Vertex (0) will sum up to 180 (π) degrees by default based on construction.
The highlighted blue and red colors at vertex (1) must sum to 180 (π).
Essentially the three red corners must sum to the complement of the blue corner.
Here are the angular relationships:
Since the right spherical triangle 0 is at the pentagon,
the B face angle is always 36 degrees.
Solve a right spherical triangle with one edge and opposing face angle.
b0 = x / 2
B0 = 36
solve triangle 0
Triangle 1 is isosceles and the 'C' angle is the complement
of the pentagon corner that sums to 180 (pi).
Solve a spherical triangle with two edges and included face angle.
a1 = b1 = 2x
C1 = 180 - A0 * 2
solve triangle 1
y = c1 / 2
Since triangle 1 is isosceles the resultant face angles A and B will be the same.
Construct spherical triangles 2, 3, and 4 which are identical.
a2 = a3 = a4 = y ( = green_x )
b2 = b3 = b4 = x ( = red )
C2 = C3 = C4 = 180 - A1
solve triangle 2, 3, 4
cos(c) = cos(a)*cos(b) + sin(a)*sin(b)*cos(C)
cos(C) = (cos(c) - cos(a)*cos(b))/( sin(a)*sin(b) )
Finish spherical triangle 5 which is equilateral:
a5 = c2
b5 = c3
c5 = c4
solve triangle 5 (three edges known)
Finally the summation of face angles at vertex 1 must be 180 (pi).
B1 + A4 + B5 + B2 == 180
or
B1 - ( A4 + B5 + B2 ) == 0
NSolve(sum_x(x) - 180° = 0, x = 14°)
Now the only question is what is the value of the edge angle x such that the summation at vertex 1 is 180.
By simply iterating the edge angle x and solving the spherical triangles to solve the 180 degree requirement at the blue vertex 1 you arrive at the value. Remember the value of edge y is not independent.
Here are the final spherical angle values for the two triangles:
x 14.495596141331275 0.252995879705616
y 16.289240170644682 0.284300873625873
TRI a b c
00 10.081227058633685 7.247798070665638 12.394269914560871
01 28.991192282662553 28.991192282662553 32.578480341289364
02 16.289240170644682 14.495596141331276 26.839102797641246
03 16.289240170644682 14.495596141331276 26.839102797641246
04 16.289240170644682 14.495596141331276 26.839102797641246
05 26.839102797641246 26.839102797641246 26.839102797641246
TRI A B C
00 54.640124510181501 36.000000000000000 90.000000000000000
01 58.172482483059767 58.172482483059767 70.719750979636999
02 31.859581862437821 28.102009218011407 121.827517516940247
03 31.859581862437821 28.102009218011407 121.827517516940247
04 31.859581862437821 28.102009218011407 121.827517516940247
05 61.865926436490909 61.865926436490909 61.865926436490909
You'll notice the geometrically derived numbers differ slightly from Taff's.
Cheers, Chris