Integration Using Trigonometric Identities

Integration using trigonometric identities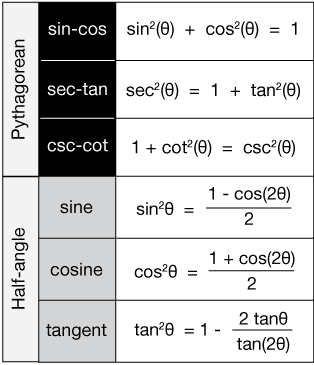 Now we'll use them to solve integrals of the type
Now we'll use them to solve integrals of the type These will be divided into two categories below, those where at least one of m or n are odd, and integrals where both m or n are even. The best way to do this is by example, so here we go. Example: ∫ tan3x dxFind the indefinite integral:
This is an example very similar to the first, but it will be a little more complicated to integrate.
First, use the Pythagorean identity for tangent and secant
These will be divided into two categories below, those where at least one of m or n are odd, and integrals where both m or n are even. The best way to do this is by example, so here we go. Example: ∫ tan3x dxFind the indefinite integral:
This is an example very similar to the first, but it will be a little more complicated to integrate.
First, use the Pythagorean identity for tangent and secant
 From this, we get two integrals, each of which can be solved by simple substitution (u-substitution). Here's what it looks like:
From this, we get two integrals, each of which can be solved by simple substitution (u-substitution). Here's what it looks like:
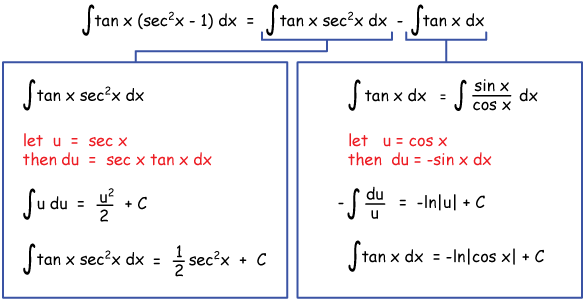 Putting it all together (and remembering that the integral on the right had a minus sign in front of it), we get the result:
Putting it all together (and remembering that the integral on the right had a minus sign in front of it), we get the result:
- Trigonometric integrals and
- Integration by substitution of trig. functions (or "trig. substitution")