Vztah mezi obvodem a obsahem kruhu
První, kdo vztah mezi obvodem a obsahem kruhu odvodil byl patrně Archimedes (287-212). Ukážeme si dvě metody, při nichž si vhodně kruh rozstříháme a přerovnáme jej do útvaru, jehož obsah známe. Aby byly naše úvahy dostatečně přesné, musí být jednotlivé dílky velmi malé. Úplně přesné to bude, až bude kruh rozstříhán na nekonečně mnoho nekonečně malých částí. To nezvládneme nůžkama, ale v naší představě by se nám to mohlo podařit.
Metoda 1
Představte si, že z kružnice o poloměru r sloupnete první slupku a rozvinete ji do úsečky, jejíž délka bude stejná jako obvod o kružnice. Pak sloupnete další slupku, ta už bude trochu menší, a pokračujete dál, dokud nám nezbyde malý kruh s poloměrem rovným tloušťce slupek. Takto jste přibližně rozvinuli kruh do rovnoramenného trojúhelníku stejného obsahu. Dostáváme tím další známou Archimedovu větu:
Obsah kruhu je roven obsahu rovnoramenného trojúhelníku, jehož základna je rovna obvodu kruhu a výška poloměru kruhu.
Metoda 2
Rozdělíme kruh jako dort na kruhové výseče a poskládáme je na tácek. Čím menší měsíčky nakrájíme, tím více se útvar, který z nich můžeme poskládat, blíží obdélníku. Kdybychom nařezali nekonečně mnoho nekonečně tenkých kousků, získali bychom přesně obdélník.
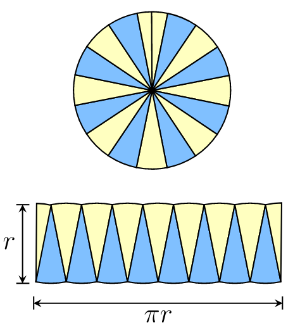
Přerovnejte dorty do obdélníkového tvaru. Rozkrájené je již máte.
Odkazy:
realisticky.cz: Matematika ZŠ, 8. ročník, kapitola "Kruh, kružnice", oddíl Obsah kruhu I, k dispozici zde