Caso 1: Planos que se cortan en un punto
Para estudiar la posición relativa
de 3 planos resolveremos el sistema formado por las 3 ecuaciones generales de
dichos planos.
Según el tipo de sistema que sea, el número de soluciones que tenga, lo
relacionaremos con el número de puntos intersección entre los 3 planos y por lo
tanto, la posición relativa entre ellos.
Cuando encuentres el recurso, selecciona los coeficientes de cada
una de las ecuaciones de los diferentes planos.
Caso 1:
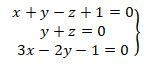
Geométricamente: hay un punto intersección
Analíticamente: el sistema tiene 1 punto solución, es un sistema compatible determinado (SCD)
Posición relativa: 3 planos que se cortan en un punto